题目内容
如图所示,⊙O内切△ABC的边于D、E、F,AB=AC,连接AD交⊙O于点H,直线HF交BC的延长线于点G.求证:
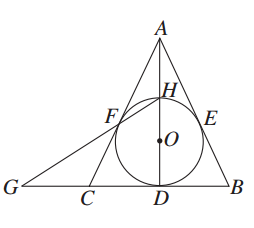
(1)圆心O在直线AD上;
(2)点C是线段GD的中点.

(1)圆心O在直线AD上;
(2)点C是线段GD的中点.
(1)见解析 (2)见解析
证明:(1)∵AB=AC,AF=AE,∴CF=BE.
又∵CF=CD,BD=BE,
∴CD=BD.
∴AD是∠CAB的平分线.
∴内切圆圆心O在直线AD上.

(2)连接DF,由(1)知,DH是⊙O的直径,
∴∠DFH=90°,
∴∠FDH+∠FHD=90°.
由题易知∠G+∠FHD=90°,
∴∠FDH=∠G.
∵⊙O与AC相切于点F,
∴∠AFH=∠GFC=∠FDH,
∴∠GFC=∠G.∴CG=CF=CD,
∴点C是线段GD的中点.
又∵CF=CD,BD=BE,
∴CD=BD.
∴AD是∠CAB的平分线.
∴内切圆圆心O在直线AD上.

(2)连接DF,由(1)知,DH是⊙O的直径,
∴∠DFH=90°,
∴∠FDH+∠FHD=90°.
由题易知∠G+∠FHD=90°,
∴∠FDH=∠G.
∵⊙O与AC相切于点F,
∴∠AFH=∠GFC=∠FDH,
∴∠GFC=∠G.∴CG=CF=CD,
∴点C是线段GD的中点.

练习册系列答案
相关题目
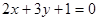 和圆
和圆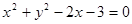 相交于点
相交于点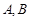 ,则弦
,则弦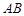 的垂直平分线的方程是_________.
的垂直平分线的方程是_________.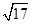 ,求直线l的倾斜角;
,求直线l的倾斜角;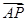 =
=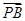 ,求此时直线l的方程.
,求此时直线l的方程. ,若在圆
,若在圆 上存在点
上存在点 ,使得
,使得 ,则
,则 的取值范围是( )
的取值范围是( )



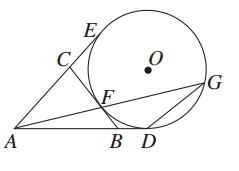
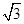 ,∠APB=30°,则AE=________.
,∠APB=30°,则AE=________.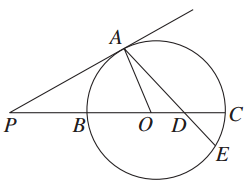
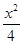 +y2=1.过
+y2=1.过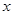 轴上的动点
轴上的动点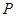 (m,0)作圆x2+y2=1的切线l交椭圆G于A,B两点.
(m,0)作圆x2+y2=1的切线l交椭圆G于A,B两点.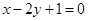 的最大距离;
的最大距离; 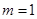 时,求A,B两点坐标;
时,求A,B两点坐标; 有公共点,则b的取值范围是( )
有公共点,则b的取值范围是( ) ,1+2
,1+2