题目内容
如图所示,AD,AE,BC分别与圆O切于点D,E,F,延长AF与圆O交于另一点G.给出下列三个结论:
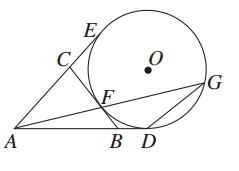
①AD+AE=AB+BC+CA;
②AF·AG=AD·AE;
③△AFB∽△ADG.
其中正确结论的序号是( )

①AD+AE=AB+BC+CA;
②AF·AG=AD·AE;
③△AFB∽△ADG.
其中正确结论的序号是( )
| A.①② | B.②③ | C.①③ | D.①②③ |
A
逐个判断:由切线定理得CE=CF,BD=BF,
所以AD+AE=AB+BD+AC+CE
=AB+AC+BC,即①正确;
由切割线定理得AF·AG=AD2=AD·AE,即②正确;
因为△ADF∽△AGD,所以③错误.故选A.
所以AD+AE=AB+BD+AC+CE
=AB+AC+BC,即①正确;
由切割线定理得AF·AG=AD2=AD·AE,即②正确;
因为△ADF∽△AGD,所以③错误.故选A.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
 中,若圆
中,若圆 的圆心在第一象限,圆
的圆心在第一象限,圆 轴相交于
轴相交于 、
、 两点,且与直线
两点,且与直线 相切,则圆
相切,则圆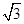 ,则直线l的方程为( )
,则直线l的方程为( )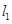 和
和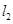 是圆
是圆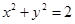 的两条切线,若
的两条切线,若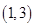 ,则
,则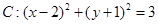 ,从点
,从点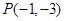 发出的光线,经
发出的光线,经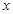 轴反射后恰好经过圆心
轴反射后恰好经过圆心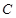 ,则入射光线的斜率为( )
,则入射光线的斜率为( )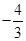



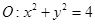 上任取一点
上任取一点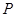 ,过点
,过点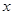 轴的垂线段
轴的垂线段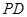 ,
,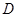 为垂足.设
为垂足.设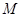 为线段
为线段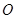 上运动时,求点
上运动时,求点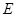 的方程;
的方程;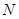 ,试判断直线
,试判断直线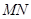 与轨迹
与轨迹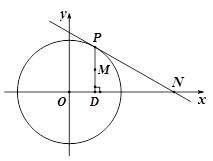
 是直线
是直线
 上一动点,
上一动点, 是圆C:
是圆C: 的两条切线,A、B是切点,若四边形
的两条切线,A、B是切点,若四边形 的最小面积是2,则
的最小面积是2,则 的值为?
的值为?