题目内容
【题目】已知函数 ,
,![]() ,
,![]() 为自然对数的底数.
为自然对数的底数.
(1)若![]() ,
,![]() ,证明:当
,证明:当![]() 时,
时,![]() 恒成立;
恒成立;
(2)若![]() ,
,![]() ,
,![]() 在
在![]() 上存在两个极值点,求
上存在两个极值点,求![]() 的取值范围.
的取值范围.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)根据导函数求出函数的单调性得函数的最值,即可得证;
(2)求出导函数,将问题转化为讨论![]() 的零点问题.
的零点问题.
解:(1)由题知![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
所以,当![]() 时,
时,![]() ,命题得证;
,命题得证;
(2)由题知:![]() ,
, ,
,
所以![]() 与
与![]() ,在
,在![]() 上正负同号,
上正负同号,
当![]() 时,
时,![]() 没有零点,
没有零点,![]() 在
在![]() 上没有极值点;
上没有极值点;
当![]() 时,令
时,令![]() ,则
,则![]()
当![]() 时,
时,![]() ,
,![]() 在
在![]() )上单调递减,
)上单调递减,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
若![]() ,即
,即![]() ,
,![]() ,
,![]() 在
在![]() 上没有极值点
上没有极值点
若![]() ,即
,即![]() ;因为
;因为![]() ,所以
,所以![]() 在
在![]() 上有1个零点
上有1个零点![]() ;
;
由(1)知:![]() 所以
所以![]() ,
,
所以![]() 在
在![]() 上也有1个零点
上也有1个零点![]() ;
;
所以,当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
当![]() 时,
时,![]() ,在
,在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() 在
在![]() 上有两个极值点:
上有两个极值点:![]() ;
;
所以![]()

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案【题目】为了解某高校学生中午午休时间玩手机情况,随机抽取了100名大学生进行调查.下面是根据调查结果绘制的学生日均午休时间的频率分布直方图,将日均午休时玩手机不低于40分钟的学生称为“手机控”.

(1)求列联表中未知量的值;
非手机控 | 手机控 | 合计 | |
男 |
|
|
|
女 |
| 10 | 55 |
合计 |
(2)能否有![]() 的把握认为“手机控与性别有关”?
的把握认为“手机控与性别有关”?
 .
.
| 0.05 | 0.10 |
| 3.841 | 6.635 |
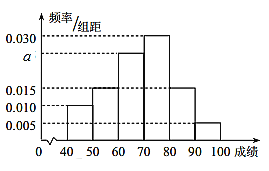
【题目】在某校举行的航天知识竞赛中,参与竞赛文科生与理科生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() ,分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图如图所示.
,分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图如图所示.
文科生 | 理科生 | 合计 | |
获奖 | 5 | ||
不获奖 | |||
合计 | 200 |
参考公式: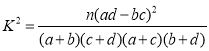 (其中
(其中![]() 为样本容量)
为样本容量)
随机变量![]() 的概率分布:
的概率分布:
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.001 | |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)求![]() 的值;
的值;
(2)填写上方的![]() 列联表,并判断能否有超过
列联表,并判断能否有超过![]() 的把握认为“获奖与学生的文、理科有关”?
的把握认为“获奖与学生的文、理科有关”?