题目内容
在直三棱柱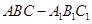 中,
中,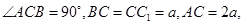
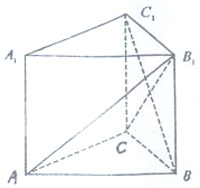
(1)求异面直线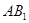 与
与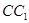 所成角的大小;
所成角的大小;
(2)求多面体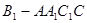 的体积。
的体积。
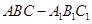 中,
中,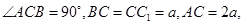

(1)求异面直线
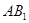 与
与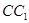 所成角的大小;
所成角的大小;(2)求多面体
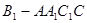 的体积。
的体积。(1) (2)
(2)
 (2)
(2)
试题分析:解:(1)由条件
 ,因此
,因此 即为异面直线
即为异面直线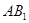 与
与 所成角。
所成角。由条件得
 ,
, ,
, ,
,在
 中,求出
中,求出 。
。  ,
, 。
。 所以异面直线
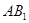 与
与 所成角的大小为
所成角的大小为 。
。 (2)由图可知,
 ,
, 由条件得
 ,
, ,
, ,
, 因此

点评:求异面直线所成的角,可通过转化为共面直线所成的角来求解,有时也可通过向量来求。

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
 中,侧棱
中,侧棱 底面
底面 ,底面
,底面 为
为 上一点,
上一点, ,
, .
.
 为
为 的中点,求证
的中点,求证 平面
平面 ;
;  的体积.
的体积. 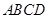 的边长为2,
的边长为2,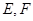 分别为边
分别为边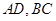 的中点,
的中点,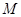 是线段
是线段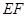 的中点,如图,把正方形沿
的中点,如图,把正方形沿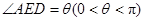 .
.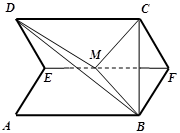
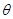 取何值,
取何值,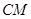 与
与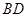 不可能垂直;
不可能垂直;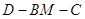 的大小为
的大小为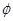 ,当
,当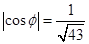 时,求
时,求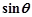 的值.
的值.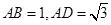 ,
,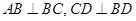 ,如图(1).把
,如图(1).把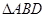 沿
沿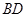 翻折,使得平面
翻折,使得平面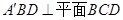 ,如图(2).
,如图(2).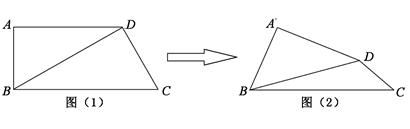
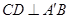 ;
;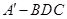 的体积;
的体积;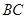 上是否存在点N,使得
上是否存在点N,使得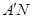
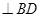 ?若存在,请求出
?若存在,请求出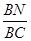 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 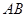 是⊙
是⊙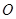 的直径,
的直径,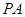 垂直于⊙
垂直于⊙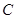 是圆周上不同于
是圆周上不同于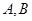 的任意一点,(1) 求证:
的任意一点,(1) 求证: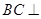 平面
平面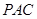 。(2) 求二面角 P-BC-A 的大小。
。(2) 求二面角 P-BC-A 的大小。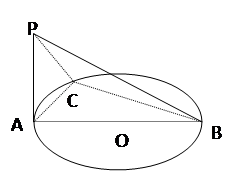



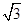 的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=
的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=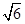 ,M,N分别为PB,PD的中点.
,M,N分别为PB,PD的中点.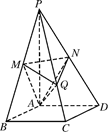
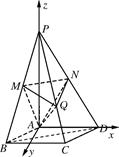
 是正方形,
是正方形,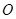 为对角线
为对角线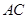 和
和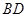 的交点,
的交点,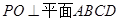 ,
,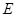 为
为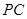 的中点;
的中点;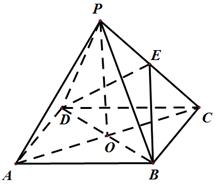
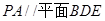 ;
;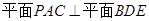 .
.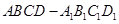 中,
中,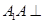 面
面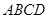 ,底面
,底面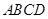 是直角梯形,
是直角梯形,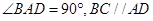 ,
,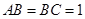 ,
,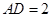 ,异面直线
,异面直线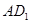 与
与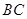 所成角为
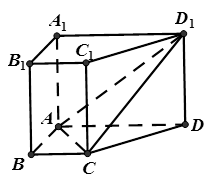
所成角为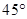 .
.
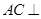 平面
平面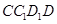 ;
;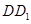 与平面
与平面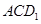 所成角的正弦值.
所成角的正弦值.