题目内容
8.已知α∈(-$\frac{π}{2}$,0),且cosα=$\frac{\sqrt{5}}{5}$,则sin(π+2α)等于( )| A. | $\frac{1}{5}$ | B. | -$\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | -$\frac{3}{5}$ |
分析 由条件利用同角三角函数的基本关系求得sinα的值,再利用诱导公式、二倍角的正弦公式,求得sin(π+2α)的值.
解答 解:∵α∈(-$\frac{π}{2}$,0),且cosα=$\frac{\sqrt{5}}{5}$,∴sinα=-$\sqrt{{1-cos}^{2}α}$=-$\frac{2\sqrt{5}}{5}$,
则sin(π+2α)=-sin2α=-2sinαcosα=-2•(-$\frac{2\sqrt{5}}{5}$)•$\frac{\sqrt{5}}{5}$=$\frac{4}{5}$,
故选:C.
点评 本题主要考查诱导公式,同角三角函数的基本关系,二倍角的正弦公式的应用,属于基础题.

练习册系列答案
相关题目
19.已知$\overrightarrow a,\overrightarrow b$满足:$\left|{\overrightarrow a}\right|=2,\left|{\overrightarrow b}\right|=1,\left|{\overrightarrow a-\overrightarrow b}\right|=\sqrt{6}$,则$\left|{\overrightarrow a+\overrightarrow b}\right|$( )
| A. | $\sqrt{3}$ | B. | $\sqrt{10}$ | C. | 3 | D. | 2 |
3.已知O是锐角△ABC的外接圆圆心,∠A=60°,$\frac{cosB}{sinC}$•$\overrightarrow{AB}$+$\frac{cosC}{sinB}$•$\overrightarrow{AC}$=m•$\overrightarrow{OA}$,则m的值为( )
| A. | -$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | -1 | D. | 1 |
20.已知a是方程x+lgx=4的根,b是方程x+10x=4的根,函数f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2+(a+b-4)x,若对任意x∈[t,t+2],不等式f(x+t)≥2f(x)恒成立,则实数t的取值范围是( )
| A. | [$\sqrt{2}$,+∞) | B. | [2,+∞) | C. | (0,2] | D. | [-$\sqrt{2}$,-1]∪[$\sqrt{2}$,$\sqrt{3}$] |
17.抛物线y=4x2的准线方程为( )
| A. | x=-1 | B. | y=-1 | C. | x=-$\frac{1}{16}$ | D. | y=-$\frac{1}{16}$ |
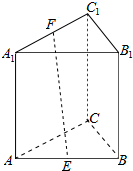 如图,正三棱柱ABC-A1B1C1的底面边长为4,侧棱长为4,E,F分别是AB,A1C1的中点,则EF的长等于2$\sqrt{5}$.
如图,正三棱柱ABC-A1B1C1的底面边长为4,侧棱长为4,E,F分别是AB,A1C1的中点,则EF的长等于2$\sqrt{5}$.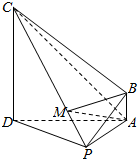 在四梭推 P-ABCD中,CD⊥平面PAD,AB∥CD,CD=4AB,AC⊥PA,M为线段CP上一点.
在四梭推 P-ABCD中,CD⊥平面PAD,AB∥CD,CD=4AB,AC⊥PA,M为线段CP上一点.