题目内容
已知椭圆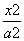
＋
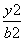＝1(a>b>0)，点
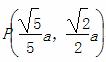在椭圆上．
(1)求椭圆的离心率；
(2)设A为椭圆的左顶点，O为坐标原点，若点Q在椭圆上且满足|AQ|＝|AO|，求直线OQ的斜率．
解：(1)因为点P
在椭圆上，故
＋
＝1，可得
＝
.
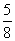于是e2＝
＝1－＝
，
所以椭圆的离心率e＝
.
(2)设直线OQ的斜率为k，则其方程为y＝kx.设点Q的坐标为(x0，y0)．
由条件得
消去y0并整理得x
＝
.①
由|AQ|＝|AO|，A(－a,0)及y0＝kx0得，
(x0＋a)2＋k2x＝a2，
整理得(1＋k2)x＋2ax0＝0.
而x0≠0，故x0＝
.
代入①，整理得(1＋k2)2＝4k2·
＋4.由(1)知＝
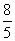，故(1＋k2)2＝
k2＋4，
即5k4－22k2－15＝0，可得k2＝5.
所以直线OQ的斜率k＝±
.
练习册系列答案
相关题目
＋
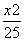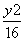＝1的左、右焦点，P为椭圆上一点，M是F1P的中点，|OM|＝3，则P点到椭圆左焦点的距离为( )
－
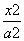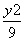＝1上一点，双曲线的一条渐近线方程为3x－2y＝0，F1，F2分别是双曲线的左，右焦点，若|PF1|＝3，则|PF2|＝( )
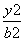＝1(a>0，b>0)的左、右焦点，过F1的直线l与双曲线的左、右两支分别交于A，B两点．若△ABF2是等边三角形，则该双曲线的离心率为________．
是第二象限，
，则
。
的值是（ ） 
B.－
D.－