题目内容
 某市的教育研究机构对全市高三学生进行综合素质测试,随机抽取了100名学生的成绩,得到如图所示的成绩频率分布直方图.
某市的教育研究机构对全市高三学生进行综合素质测试,随机抽取了100名学生的成绩,得到如图所示的成绩频率分布直方图.(Ⅰ)估计这100名学生中综合素质成绩在80分以上的人数;
(Ⅱ)若评定成绩不低于80分为优秀.视频率为概率,从全市学生中任选3名学生(看作有放回的抽样),变量ξ表示3名学生中成绩优秀的人数,求变量ξ的分布列及期望E(ξ).
考点:离散型随机变量的期望与方差,频率分布直方图
专题:概率与统计
分析:(Ⅰ)利用频率分布直方图能求出这100名学生中综合素质成绩在80分以上的人数.
(Ⅱ)由题意知ξ~B(3,0.3),由此能求出变量ξ的分布列及期望E(ξ).
(Ⅱ)由题意知ξ~B(3,0.3),由此能求出变量ξ的分布列及期望E(ξ).
解答:
解:(Ⅰ)这100名学生中综合素质成绩在80分以上的人数为:
100×[(0.022+0,008)×10]=30(人).
∴这100名学生中综合素质成绩在80分以上的人数为30人.
(Ⅱ)由题意知ξ=0,1,2,3,
设事件A表示“抽到的学生是优秀学生”,则P(A)=0.3,P(
)=0.7,
∴ξ~B(3,0.3),
∴P(ξ=0)=
0.73=0.343,
P(ξ=1)=
•0.3•0.72=0.441,
P(ξ=2)=
0.32•0.7=0.189,
P(ξ=3)=
0.33=0.027.
∴ξ的分布列为:
∵ξ~B(3,0.3),∴Eξ=3×0.3=0.9.
100×[(0.022+0,008)×10]=30(人).
∴这100名学生中综合素质成绩在80分以上的人数为30人.
(Ⅱ)由题意知ξ=0,1,2,3,
设事件A表示“抽到的学生是优秀学生”,则P(A)=0.3,P(
. |
| A |
∴ξ~B(3,0.3),
∴P(ξ=0)=
| C | 0 3 |
P(ξ=1)=
| C | 1 3 |
P(ξ=2)=
| C | 2 3 |
P(ξ=3)=
| C | 3 3 |
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | 0.343 | 0.441 | 0.189 | 0.027 |
点评:本题考查频率分布直方图的应用,考查离散型随机变量的分布列和数学期望的求法,解题时要认真审题,注意二项分布的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
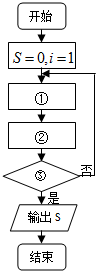 画出一个计算1+
画出一个计算1+