题目内容
12.如果函数y=f(x)的导函数f′(x)的图象如图所示,给出下列判断: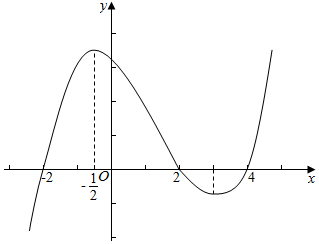
①函数y=f(x)在区间$(-3,-\frac{1}{2})$内单调递增;
②函数y=f(x)在区间(4,5)内单调递增;
③函数y=f(x)的最小值是f(-2)和f(4)中较小的一个;
④函数y=xf′(x)在区间(-3,-2)内单调递增;
⑤函数y=xf′(x)在区间$(-\frac{1}{2},3)$内有极值点;
则上述判断中正确的是②③⑤.
分析 根据函数单调性和导数之间的关系分别判断函数的导数的符号即可得到结论.
解答 解:①函数y=f(x)在区间(-3,-2)上f′(x)<0,函数为减函数,则①错误;
②函数y=f(x)在区间(4,5)内f′(x)>0,则函数单调递增;故②正确,
③由图象知当x=-2或4时,函数f(x)取得极小值,则函数y=f(x)的最小值是f(-2)和f(4)中较小的一个,③正确;
④函数y=xf′(x)在区间(-3,-2)的导数为y′=f′(x)+x[f′(x)]′,
∵当-3<x<-2时,f′(x)<0,且f′(x)为增函数,∴[f′(x)]′>0,
∴y′=f′(x)+x[f′(x)]′<0,即y=xf'(x)在区间(-3,-2)上单调递减,故④错误,
⑤函数y=xf′(x)的导数y′=f′(x)+x[f′(x)]′,
当-$\frac{1}{2}$<x<0时,f′(x)>0,f′(x)为减函数,∴[f′(x)]′<0,
此时y′=f′(x)+x[f′(x)]′>0此时函数y=xf'(x)为增函数,
当2<x<3时,f′(x)<0,f′(x)为减函数,∴[f′(x)]′<0,
此时y′=f′(x)+x[f′(x)]′<0此时函数y=xf'(x)为减函数,
则函数y=xf'(x)在区间$(-\frac{1}{2},3)$内有极值点;故⑤正确,
故答案为:②③⑤.
点评 本题主要考查命题的真假判断,涉及函数单调性和导数,极值和导数之间的关系,考查学生的识图和用图的能力.综合性较强,有一定的难度.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
20.若实数x,y满足约束条件$\left\{\begin{array}{l}{3x-y≥0}\\{x+y-4≤0}\\{2y≥{x}^{2}}\end{array}\right.$,则4y-x的取值范围是( )
| A. | [-$\frac{1}{2}$,16] | B. | [$\frac{1}{2}$,16] | C. | [$\frac{1}{2}$,4] | D. | [1,16] |
7.向量$\overrightarrow a=({2,-1,3})$,向量$\overrightarrow b=({4,-2,k})$,且满足向量$\overrightarrow a⊥\overrightarrow b$,则k等于( )
| A. | 6 | B. | -6 | C. | $-\frac{10}{3}$ | D. | -2 |
17.从2016年1月1日起,广东、湖北等18个保监局所辖地区将纳入商业车险改革试点范围,其中最大的变化是上一年的出险次数决定了下一年的保费倍率,具体关系如表:
经验表明新车商业险保费与购车价格有较强的线性关系,下面是随机采集的8组数据(x,y)(其中x(万元)表示购车价格,y(元)表示商业车险保费):(8,2150)、(11,2400)、(18,3140)、(25,3750)、(25,4000)、(31,4560)、(37,5500)、(45,6500),设由着8组数据得到的回归直线方程为:$\widehat{y}$=b$\widehat{x}$+1055.
(1)求b;
(2)广东李先生2016年1月购买一辆价值20万元的新车
①估计李先生购车时 的商业车险保费;
②若该车今年2月份已出过一次险,现在有被刮花了,李先生到汽车维修4S店询价,预计修车费用为800元,保险专家建议李先生自费(即不出险),你认为李先生是否应该接受建议?说明理由.(假设车辆下一年与上一年都购买相同的商业车险产品进行续保)
| 上一年出险次数 | 0 | 1 | 2 | 3 | 4 | 5次以上(含5次) |
| 下一年保费倍率 | 85% | 100% | 125% | 150% | 175% | 200% |
| 连续两年没出险打7折,连续三年没出险打6折 | ||||||
(1)求b;
(2)广东李先生2016年1月购买一辆价值20万元的新车
①估计李先生购车时 的商业车险保费;
②若该车今年2月份已出过一次险,现在有被刮花了,李先生到汽车维修4S店询价,预计修车费用为800元,保险专家建议李先生自费(即不出险),你认为李先生是否应该接受建议?说明理由.(假设车辆下一年与上一年都购买相同的商业车险产品进行续保)
 如图,AB是圆柱的直径且AB=2,PA是圆柱的母线且PA=2,点C是圆柱底面圆周上的点.
如图,AB是圆柱的直径且AB=2,PA是圆柱的母线且PA=2,点C是圆柱底面圆周上的点.