题目内容
20.若实数x,y满足约束条件$\left\{\begin{array}{l}{3x-y≥0}\\{x+y-4≤0}\\{2y≥{x}^{2}}\end{array}\right.$,则4y-x的取值范围是( )| A. | [-$\frac{1}{2}$,16] | B. | [$\frac{1}{2}$,16] | C. | [$\frac{1}{2}$,4] | D. | [1,16] |
分析 令z=y-x,作平面区域,从而结合图象知,要分类讨论求z的最值,从而结合图象求取值范围即可.
解答 解:令z=y-x,由题意作平面区域如下,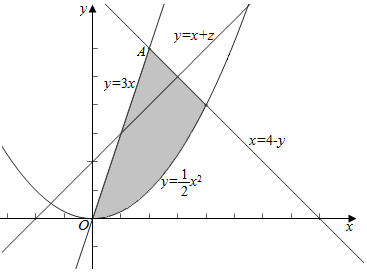 ,
,
当直线y=x+z与y=$\frac{{x}^{2}}{2}$相切时,z有最小值,
而y′=x=1得,切点为(1,$\frac{1}{2}$);
故z的最小值为$\frac{1}{2}$-1=-$\frac{1}{2}$;
当直线y=x+z过点A(1,3)时,z有最大值3-1=2;
故-$\frac{1}{2}$≤y-x≤2,
故$\frac{1}{2}$≤4y-x≤16,
故选:B.
点评 本题考查了线性规划的变形应用及导数的综合应用,同时考查了数形结合的思想方法应用,属于中档题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
11.在△ABC中,A=$\frac{π}{3}$,|$\overrightarrow{AC}$|=m,m∈[1,2],若对于任意实数t恒有|$\overrightarrow{AB}$-t$\overrightarrow{AC}$|≥|$\overrightarrow{BC}$|,则△ABC面积的最大值是( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
12.等差数列的第1项是7,第9项是1,则它的第5项是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |