题目内容
2.已知不等式|2x-1|-|x+1|<2的解集为{x|a<x<b}.(1)求a,b的值;
(2)已知x>y>z,求证:存在实数k,使$-\frac{3a}{{2({x-y})}}+\frac{b}{{4({y-z})}}≥\frac{k}{x-z}$恒成立,并求k的最大值.
分析 (1)把要求得不等式去掉绝对值,化为与之等价的3个不等式组,求得每个不等式组的解集,再取并集,即得所求.
(2)由条件可得存在实数k,使得$\frac{1}{x-y}$+$\frac{1}{y-z}$≥$\frac{k}{x-z}$,利用基本不等式从而证得结论,可得k的最大值为4.
解答 解:(1)由不等式|2x-1|-|x+1|<2,可得$\left\{\begin{array}{l}{x<-1}\\{1-2x-(-x-1)<2}\end{array}\right.$①,或$\left\{\begin{array}{l}{-1≤x≤\frac{1}{2}}\\{1-2x-(x+1)<2}\end{array}\right.$②,
或$\left\{\begin{array}{l}{x>\frac{1}{2}}\\{2x-1-(x+1)<2}\end{array}\right.$ ③.
解①求的x∈∅,解②求得-$\frac{2}{3}$<x≤$\frac{1}{2}$,解③求得$\frac{1}{2}$<x<4,
综上可得,-$\frac{2}{3}$<x<4.
再根据不等式的解集为{x|a<x<b},可得a=-$\frac{2}{3}$,b=4.
(2)由题意,$-\frac{3a}{{2({x-y})}}+\frac{b}{{4({y-z})}}≥\frac{k}{x-z}$恒成立,即存在实数k,使得$\frac{1}{x-y}$+$\frac{1}{y-z}$≥$\frac{k}{x-z}$
∵x>y>z,∴x-y>0,y-z>0,x-z>0,
∴[(x-y)+(y-z)]($\frac{1}{x-y}$+$\frac{1}{y-z}$)=2+$\frac{y-z}{x-y}$+$\frac{x-y}{y-z}$≥4,当且仅当$\frac{y-z}{x-y}$=$\frac{x-y}{y-z}$时取等号,即$\frac{1}{x-y}$+$\frac{1}{y-z}$≥$\frac{4}{x-z}$
故存在实数k≤4,使$-\frac{3a}{{2({x-y})}}+\frac{b}{{4({y-z})}}≥\frac{k}{x-z}$恒成立,k的最大值为4.
点评 本题主要考查绝对值不等式的解法,不等式的性质应用,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | ($\frac{π}{3}$,$\frac{5π}{6}$) | B. | ($\frac{π}{6}$,$\frac{2π}{3}$) | C. | ($\frac{π}{2}$,π) | D. | ($\frac{2π}{3}$,π) |
| A. | (-$\frac{1}{2016}$,+∞) | B. | (-$\frac{1}{3}$,+∞) | C. | (-$\frac{1}{2}$,+∞) | D. | (-$\frac{1}{4}$,+∞) |
| A. | 336 | B. | 408 | C. | 240 | D. | 264 |
| A. | 3$\sqrt{6}$ | B. | 4$\sqrt{6}$ | C. | 6$\sqrt{6}$ | D. | 12$\sqrt{6}$ |
| A. | 1≤a≤9 | B. | 6<a<9 | C. | 6≤a≤9 | D. | a≤9 |
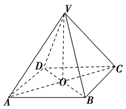 如图所示,四棱锥V-ABCD的底面为边长等于2cm的正方形,顶点V与底面正方形中心的连线为棱锥的高,侧棱长VC=4cm,求这个正四棱锥的体积.
如图所示,四棱锥V-ABCD的底面为边长等于2cm的正方形,顶点V与底面正方形中心的连线为棱锥的高,侧棱长VC=4cm,求这个正四棱锥的体积.