题目内容
函数 ,求该函数的最大值和最小值以及取得最值时的
,求该函数的最大值和最小值以及取得最值时的 的值.
的值.
 ,求该函数的最大值和最小值以及取得最值时的
,求该函数的最大值和最小值以及取得最值时的 的值.
的值.t= 时f(x)max=
时f(x)max= ,此时x=
,此时x= 或x=
或x=
当t=- 时 f(x)min=
时 f(x)min= -
- ,此时x=-
,此时x=-
 时f(x)max=
时f(x)max= ,此时x=
,此时x= 或x=
或x=
当t=-
 时 f(x)min=
时 f(x)min= -
- ,此时x=-
,此时x=-
试题分析:
 =2cos2x+2sinx+1=-2sin2x+2sinx+3=-2(sinx-
=2cos2x+2sinx+1=-2sin2x+2sinx+3=-2(sinx- )2+
)2+ 3分
3分设t= sinx,∵xÎ[-
 ,
, ]∴tÎ[-
]∴tÎ[- ,1] 6分
,1] 6分∴t=
 时f(x)max=
时f(x)max= ,此时x=
,此时x= 或x=
或x= 9分
9分当t=-
 时 f(x)min=
时 f(x)min= -
- ,此时x=-
,此时x=- 12分
12分点评:解决的关键是能根据二次函数的性质,结合整体代换的思想来求解最值,属于常规试题。

练习册系列答案
相关题目
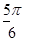 )的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得图像向左平移
)的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得图像向左平移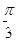 个单位,则所得函数图像对应的解析式是
个单位,则所得函数图像对应的解析式是 



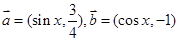 .
.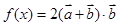
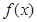 的增区间;
的增区间;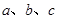 ,若
,若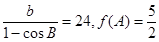 ,求边长
,求边长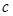
 + sin2α﹣3sinα•cosα的值。
+ sin2α﹣3sinα•cosα的值。 ,1),求
,1),求 的值
的值 .
. 的单调减区间是
的单调减区间是  ,
,

 .(Ⅰ)求
.(Ⅰ)求 函数图象的对称轴方程;(Ⅱ)求
函数图象的对称轴方程;(Ⅱ)求 时,求函数
时,求函数 的最大值,最小值.
的最大值,最小值. 的最小正周期和最小值;
的最小正周期和最小值; 上的单调递增区间.
上的单调递增区间.