题目内容
6.已知函数y=ax,y=xb,y=logcx的图象如图所示,则a,b,c的大小关系为b<a<c.(用“<”号连接)
分析 利用指数函数,对数函数,幂函数的性质,推出a,b,c的范围判断即可.
解答 解:函数y=ax,y=xb,y=logcx的图象如图所示,
由指数函数y=ax,x=2时,y∈(1,2);对数函数y=logcx,x=2,y∈(0,1);幂函数y=xb,x=2,y∈(1,2);
可得a∈(1,2),b∈(0,1),c∈(2,+∞).
可得b<a<c
故答案为:b<a<c.
点评 本题考查指数函数、对数函数、幂函数的性质的应用,考查计算能力.

练习册系列答案
相关题目
16.在△ABC中,角A,B,C所对的边分别为a,b,c,且bcosC+ccosB=$\sqrt{2}$acosC,则角C为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
17.在四面体S-ABC中,$AB⊥BC,AB=BC=\sqrt{2},SA=SC=2$,二面角S-AC-B的余弦值为$-\frac{{\sqrt{3}}}{3}$,则该四面体外接球的表面积是( )
| A. | $8\sqrt{6}π$ | B. | $\sqrt{6}π$ | C. | 24π | D. | 6π |
14.下列函数中,既是奇函数又在定义域内单调递增的是( )
| A. | y=x3 | B. | y=tanx | C. | $y={(\frac{1}{2})^x}$ | D. | y=lnx |
11.设点A,B的坐标分别为(4,0),(-4,0),直线AP,BP相交于点P,且它们的斜率之积为实数m,关于点P的轨迹下列说法正确的是( )
| A. | 当m<-1时,轨迹为焦点在x轴上的椭圆(除与x轴的两个交点) | |
| B. | 当-1<m<0时,轨迹为焦点在y轴上的椭圆(除与y轴的两个交点) | |
| C. | 当m>0时,轨迹为焦点在x轴上的双曲线(除与x轴的两个交点) | |
| D. | 当0<m<1时,轨迹为焦点在y轴上的双曲线(除与y轴的两个交点) |
18.若f(x)=2cos(ωx+φ)+k,对任意实数t都有$f(\frac{π}{3}+t)=f(\frac{π}{3}-t)$成立,且$f(\frac{π}{3})=-1$,则实数k的值等于( )
| A. | -3或1 | B. | 1 | C. | -1或3 | D. | -3 |
前不久商丘市因环境污染严重被环保部约谈后,商丘市近期加大环境治理力度,下表提供了商丘某企业节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(Ⅰ)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程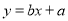 ;
;
(Ⅱ)已知该企业技改前100吨甲产品的生产能耗为90吨标准煤,试根据(Ⅰ)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低了多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)参考公式: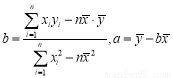
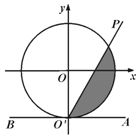 如图,在平面直角坐标系xOy中,单位圆O与y轴负半轴交于点O',过点O'作与x轴平行的直线AB,射线O'P从O'A出发,绕着点O'逆时针方向旋转至O'B,在旋转的过程中,记∠AO'P=x(0<x<π),O'P所经过的在单位圆O内区域(阴影部分)的面积为S.
如图,在平面直角坐标系xOy中,单位圆O与y轴负半轴交于点O',过点O'作与x轴平行的直线AB,射线O'P从O'A出发,绕着点O'逆时针方向旋转至O'B,在旋转的过程中,记∠AO'P=x(0<x<π),O'P所经过的在单位圆O内区域(阴影部分)的面积为S.