题目内容

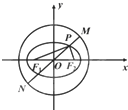如图，已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）和圆O：x2+y2=a2+b2，椭圆C的左右焦点分别为F1、F2，过椭圆上一点P和原点O的直线交圆O于M、N两点．若|PF1|•|PF2|=5，则|PM|•|PN|的值为（　　）
A、1B、3C、5D、10
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：设出P的坐标，把P的纵坐标用横坐标表示，然后由焦半径公式及|PF1|•|PF2|=5求得P的横纵坐标的平方和，由对称性得到|PM|•|PN|=a2+b2-|OM|2=a2+b2-x02-y02，代入横纵坐标的平方和后整理得答案．
解答： 解：设P（x0，y0），
∵P在椭圆上，∴
x02
a2
+
y02
b2
=1，则y02=b2(1-
x02
a2
)=b2-
a2b2
c2
+
5b2
c2
，
∵|PF1|•|PF2|=5，∴（a+ex0）（a-ex0）=5，即x02=
a2-5
c2
a2
=
a4
c2
-
5a2
c2
．
由对称性得|PM|•|PN|=a2+b2-|OM|2=a2+b2-x02-y02
=a2+b2-
a4
c2
+
5a2
c2
-b2+
a2b2
c2
-
5b2
c2
=a2-
a4
c2
+
5a2
c2
+
a2b2
c2
-
5b2
c2

=a2-
a2(a2-b2)
c2
+
5(a2-b2)
c2
=a2-a2+
5c2
c2
=5．
故选：C．
点评：本题考查了椭圆的简单几何性质，考查了焦半径公式的应用，考查了计算能力，是中档题．
练习册系列答案
相关题目
已知函数f（x）=x2+2x-2，x∈（-3，1]，则f（x）的值域为
 
．
i是虚数单位，复数z=
k-i
i
在复平面内对应的点在第三象限，则实数k的范围是（　　）
A、k≥0B、k＞0
C、k≤0D、k＜0
已知函数f（x）=lnx+
m
2x
，g（x）=x-2m，其中m∈R，e=2.71828…为自然对数的底数．
（Ⅰ）当m=1时，求函数f（x）的极小值；
（Ⅱ）对?x∈[
1
e
，1]，是否存在m∈（
1
2
，1），使得f（x）＞g（x）+1成立？若存在，求出m的取值范围；若不存在，请说明理由；
（Ⅲ）设F（x）=f（x）g（x），当m∈（
1
2
，1）时，若函数F（x）存在a，b，c三个零点，且a＜b＜c，求证：0＜a＜
1
e
＜b＜1＜c．
已知函数f（x）=
-x2-4x，x≤0
lnx，x＞0
，若f（x）≤a|x|对任意实数x都成立，则实数a的最小值为
 
．
在复平面内作出表示下列各复数的点
（1）z1=2+2i  
（2）z2=-3+i   
（3）z3=-i．
已知函数f（x）=x3+（a-1）x+1
（1）若f（x）在R上递增，求a的取值范围；
（2）若f（x）在（-1，1）上递减，求a的取值范围；
（3）若f（x）在（-1，1）上不单调，求a的取值范围；
（4）若（-1，1）为f（x）的递减区间，求a的取值范围．
设抛物线y2=2px（p＞0）的轴和它的准线交于E点，经过交点F的直线交抛物线于P、Q两点（直线PQ与抛物线的轴不垂直），则∠FEP与∠QEF的大小关系为（　　）
A、∠FEP＞∠QEF
B、∠FEP＜∠QEF
C、∠FEP=∠QEF
D、不确定
椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的左顶点A，下、上顶点B、C，右焦点F，AC与BF交于D，若|BF|=
1
3
|DF|，则椭圆的离心率等于（　　）
A、
1
2
B、
2
2
C、
1
3
D、
3
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网