题目内容
已知p:“对任意的x∈[2,4],log2x-a≥0”,q:“存在x∈R,x2+2ax+2-a=0”,若p,q均为命题,而且“p且q”是真命题,则实数a的取值范围是 .
考点:复合命题的真假
专题:常规题型,简易逻辑
分析:先由“p且q”是真命题,分析出p为真命题,q也为真命题,然后分别求出p、q为真命题的a的范围,求交集即可.
解答:
解:∵“p且q”是真命题,
∴p为真命题,q也为真命题,
由p为真命题得:a≤log2x在x∈[2,4]时恒成立,
∴a≤1-------------------①
由q为真命题,即存在x∈R,x2+2ax+2-a=0,
∴4a2-4(2-a)≥0,解得:a≥1或a≤-2------------②
由①②得:a≤-2或a=1,
故答案为:a≤-2或a=1.
∴p为真命题,q也为真命题,
由p为真命题得:a≤log2x在x∈[2,4]时恒成立,
∴a≤1-------------------①
由q为真命题,即存在x∈R,x2+2ax+2-a=0,
∴4a2-4(2-a)≥0,解得:a≥1或a≤-2------------②
由①②得:a≤-2或a=1,
故答案为:a≤-2或a=1.
点评:本题考查了复合命题的真假的判断,解题的关键是把复合命题的真假问题转化成单个命题的真假问题解决.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
利用独立性检验来考虑两个分类变量X和Y是否有关系时,通过查阅下表来确定断言“X和Y有关系”的可信度.如果k>5.024,那么就有把握认为“X和Y有关系”的百分比为( )
| P(k2>k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
| A、25% | B、75% |
| C、2.5% | D、97.5% |
命题“三角形是最多只有一个角为钝角”的否定是( )
| A、有两个角为钝角 |
| B、有三个有为钝角 |
| C、至少有两个角为钝角 |
| D、没有一个角为钝角 |
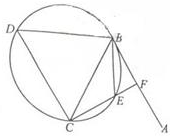 如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.