题目内容
已知不等式
>1-a
(1)若a=x,求关于x不等式的解集;
(2)若a≠1,求关于x不等式的解集.
| a |
| x-2 |
(1)若a=x,求关于x不等式的解集;
(2)若a≠1,求关于x不等式的解集.
考点:其他不等式的解法
专题:不等式的解法及应用
分析:(1)若a=x,根据分式不等式的解法,即可求关于x不等式的解集;
(2)若a≠1,讨论a的取值范围,即可求关于x不等式的解集.
(2)若a≠1,讨论a的取值范围,即可求关于x不等式的解集.
解答:
解:(1)a=x,则
>1-x,移项通分
=
>0,
由x2-2x+2=(x-1)2+1>0,
得x>2 故不等式的解集为{x|x>2}.
(2)已知a≠1,则
>1-a?
>0,
①a>1 时,可转化为(x-2)(x-
)>0?(x-2)[x-(1-
)]>0,
此时1-
<2,不等式的解集为{x|x2}
②a<1 时,可转化为(x-2)[x-(1-
)]2,
即0<a<1 时,不等式的解集为{x|2<x<1-
}
ii)当1-
=2,即a=0 时,不等式的解集为∅
iii)当1-
<2,即a<0 时,不等式的解集为{x|1-
<x<2}
当0<a<1 时,解集为 {x|2<x<1-
},
当a=0 时,不等式的解集为∅,
当a<0 时,不等式的解集为{x|1-
<x<2}.
| x |
| x-2 |
| x-(x-2)(1-x) |
| x-2 |
| x2-2x+2 |
| x-2 |
由x2-2x+2=(x-1)2+1>0,
得x>2 故不等式的解集为{x|x>2}.
(2)已知a≠1,则
| a |
| x-2 |
| (a-1)x-(a-2) |
| x-2 |
①a>1 时,可转化为(x-2)(x-
| a-2 |
| a-1 |
| 1 |
| a-1 |
此时1-
| 1 |
| a-1 |
②a<1 时,可转化为(x-2)[x-(1-
| 1 |
| a-1 |
即0<a<1 时,不等式的解集为{x|2<x<1-
| 1 |
| 1-a |
ii)当1-
| 1 |
| a-1 |
iii)当1-
| 1 |
| a-1 |
| 1 |
| 1-a |
当0<a<1 时,解集为 {x|2<x<1-
| 1 |
| 1-a |
当a=0 时,不等式的解集为∅,
当a<0 时,不等式的解集为{x|1-
| 1 |
| 1-a |
点评:本题主要考查分式不等式的解法,利用分类讨论是解决本题的关键.

练习册系列答案
相关题目
若梯形的中位线被它的两条对角线三等分,则梯形的上底a与下底b(a<b)的比是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
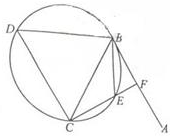 如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.