题目内容

已知△ABC的三边分别为a，b，c，面积S=（a-b+c）（a+b-c），b+c=8，则S的最大值为
 
．
考点：余弦定理,正弦定理
专题：三角函数的求值
分析：利用三角形面积公式表示出S，利用余弦定理表示出cosA，将已知第一个等式右边变形后，将表示出S与b2+c2-a2代入，整理后求出tan
A
2
的值，利用万能公式求出sinA的值，再利用基本不等式求出ab的最大值，即可确定出S的最大值．
解答： 解：∵S=
1
2
bcsinA，cosA=
b2+c2-a2
2bc
，
∴S=（a-b+c）（a+b-c）=a2-（b-c）2=a2-b2+2bc-c2=-（b2+c2-a2）+2bc=-2bccosA+2bc=2bc（1-cosA）=
1
2
bcsinA，
整理得：2（1-cosA）=
1
2
sinA，即2（1-1+2sin2
A
2
）=4sin2
A
2
=sin
A
2
cos
A
2
，
整理得：tan
A
2
=
1
4
，
∴sinA=
2tan
A
2
1+tan2
A
2
=
2×
1
4
1+(
1
4
)2
=
8
17
，
∵ab≤（
a+b
2
）2，a+b=8，
∴ab≤16，
则Smax=
1
2
×16×
8
17
=
64
17
．
故答案为：
64
17
点评：此题考查了余弦定理，以及三角函数的恒等变换，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
当0＜x＜
π
2
时，函数f（x）=
3sin2x+1
tanxcos2x
的最小值为（　　）
A、2
B、2
3
C、4
D、4
3
已知函数f（x）=ln（x+1）+mx（m∈R）．
（Ⅰ）当x=1时，函数f（x）取得极大值，求实数m的值；
（Ⅱ）已知结论：若函数f（x）=ln（x+1）+mx（m∈R）在区间（a，b）内存在导数，则存在x0∈（a，b），使得f′（x0）=
f(b)-f(a)
b-a
．试用这个结论证明：若函数g（x）=
f(x1)-f(x2)
x1-x2
（x-x1）+f（x1），（其中x2＞x1＞-1），则对任意x∈（x1，x2），都有f（x）＞g（x）；
（Ⅲ）已知正数λ1，λ2满足λ1+λ2=1，求证：对任意的实数x1，x2，若x2＞x1＞-1时，都有f（λ1x1+λ2x2）＞λ1f（x1）+λ2f（x2）．
设x，y满足约束条件
x-2y+2≥0
x+y≥1
2x+y≤4
，则z=3x-2y的最大值为
 
．
已知tanα=2
（1）求
sinα+cosα
sinα-cosα
的值；
（2）求
1
2sinαcosα+cos2α
的值．
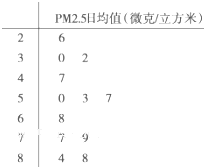PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物，根据现行国家标准GB3095-2012，PM2.5日均值在35微克/立方米以下空气质量为一级；在35微克/立方米～75毫克/立方米之间空气质量为二级；在75微克/立方米以上空气质量为超标．从某自然保护区2012年全年每天的PM2.5监测值数据中随机地抽取12天的数据作为样本，监测值如茎叶图所示（十位为茎，个位为叶）：
（Ⅰ）求空气质量为超标的数据的平均数与方差；
（Ⅱ）从空气质量为二级的数据中任取2个，求这2个数据的和小于100的概率；
（Ⅲ）以这12天的PM2.5日均值来估计2012年的空气质量情况，估计2012年（按366天算）中大约有多少天的空气质量达到一级或二级．
求满足下列条件的曲线方程：
（1）设抛物线的顶点在原点，准线方程为x=-2，求抛物线的方程；
（2）已知双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的实轴长为4
3
，焦点到渐近线的距离为
3
，求双曲线方程．
已知A，B，C为△ABC的三个内角，其对边分别为a，b，c，函数f（x）=2cosxsin（x-A）+sinA在x=
5π
12
处取得最大值．
（Ⅰ）求函数f（x）在区间[0，
π
2
]上的最小值；
（Ⅱ）若sinB+sinC=
13
3
14
，a=7，求△ABC的面积．
设△ABC的内角A、B、C所对的边分别为a，b，c，若sinB+sinC=2sinA，3a=5c，则角B=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网