题目内容
13．画出下列函数的图象，并根据图象写出单调减区间和值域．（1）y=1+$\frac{|x|-x}{2}$；
（2）y=|x2-x|．
分析 （1）作函数y=1+$\frac{|x|-x}{2}$的图象，从而写出单调减区间和值域．
（2）作函数y=|x2-x|的图象，从而写出单调减区间和值域．
解答 解：（1）作函数y=1+$\frac{|x|-x}{2}$的图象如下，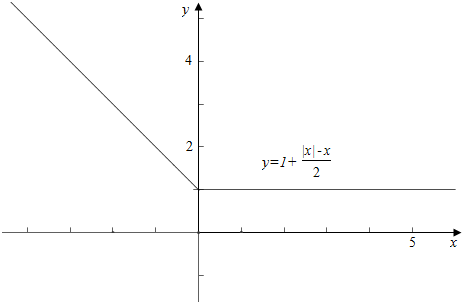
，
故函数的单调减区间为（-∞，0），值域为[1，+∞）；
（2）作函数y=|x2-x|的图象如下，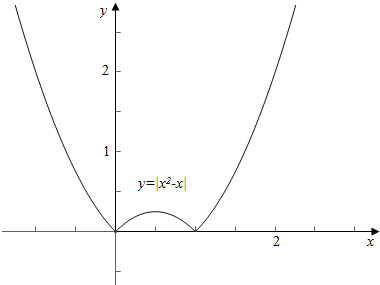
故函数的单调减区间为（-∞，0），（$\frac{1}{2}$，1）；
值域为[0，+∞）．
点评 本题考查了学生的作图能力与应用图象的能力．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
1．下边是某个学生在学习《函数的最值》一节以后做的作业，其解答过程和结论都是正确的，但是不知道什么原因，题目中定义域部分[0，█]看不清楚，请你根据所学的只是，判断一下图中“█”的可能取值．
| 已知函数y=x2-3x-4 |
| 定义域为[0，█]，求函数的值域 |
| 解：… |
| … |
| … |
| … |
| … |
| 故函数的值域为[-$\frac{25}{4}$，-4] |