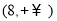题目内容
(本小题满分12分)已知向量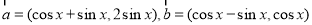 .令
.令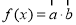 ,
,
(1)求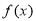 的最小正周期;
的最小正周期;
(2)当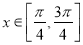 时,求
时,求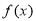 的最小值以及取得最小值时
的最小值以及取得最小值时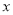 的值.
的值.
(1)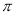 ;(2)当
;(2)当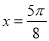 时,函数
时,函数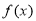 取得最小值
取得最小值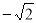 .
.
【解析】
试题分析:本题主要考查倍角公式、两角和的正弦公式、三角函数的周期、单调性、最值等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力. 先利用平方差公式把原式展开,再利用倍角公式进行化简,最后利用两角和的正弦公式将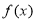 化简成
化简成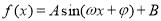 的形式,第一问,由最小正周期公式得出结果;第二问,借助于三角函数的图象判断出函数
的形式,第一问,由最小正周期公式得出结果;第二问,借助于三角函数的图象判断出函数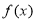 的单调性,求出函数
的单调性,求出函数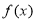 的单调区间,从而确定出函数
的单调区间,从而确定出函数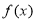 最大值的位置,同时求出最大值.
最大值的位置,同时求出最大值.
试题解析: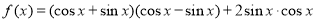 .2分
.2分
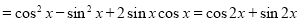 ...4分
...4分
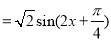 5分
5分
(1)由最小正周期公式得: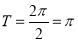 6分
6分
(2)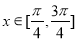 ,则
,则 7分
7分
令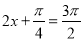 ,则
,则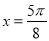 , .8分
, .8分
从而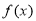 在
在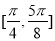 单调递减,在
单调递减,在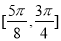 单调递增 .10分
单调递增 .10分
即当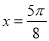 时,函数
时,函数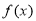 取得最小值
取得最小值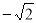 12分
12分
考点: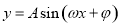 的图象及性质.
的图象及性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,函数
,函数 ,则
,则 的值等于( )
的值等于( ) B.
B. C.
C. D.
D.
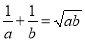 ,且
,且 ,求
,求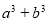 的最小值.
的最小值.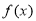 是定义在R上的奇函数,当
是定义在R上的奇函数,当 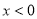 时
时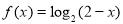 ,则
,则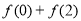 的值为_____.
的值为_____.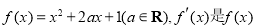 的导函数.
的导函数.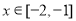 ,不等式
,不等式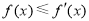 恒成立,求a的取值范围;
恒成立,求a的取值范围;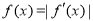 ;
;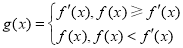 ,求
,求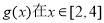 时的最小值.
时的最小值. ,且
,且 ,则实数
,则实数 ____________.
____________. 的前
的前 项和为
项和为 ,且
,且 ,则公差
,则公差 等于( )
等于( ) C.
C. D.3
D.3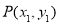 与
与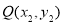 之间的“直角距离”为
之间的“直角距离”为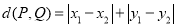 .给出下列命题:
.给出下列命题: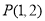 ,
,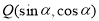
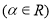 ,则
,则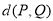 的最大值为
的最大值为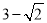 ;
;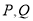 是圆
是圆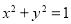 上的任意两点,则
上的任意两点,则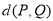 的最大值为
的最大值为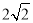 ;
; ,点
,点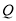 为直线
为直线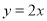 上的动点,则
上的动点,则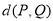 的最小值为
的最小值为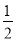 .
.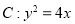 ,点
,点 ,O为坐标原点,若在抛物线C上存在一点
,O为坐标原点,若在抛物线C上存在一点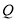 ,使得
,使得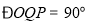 ,则实数m的取值范围是( )
,则实数m的取值范围是( )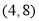 (B)
(B)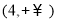 (C)
(C)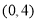 (D)
(D)