题目内容
(本小题满分14分)已知函数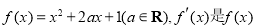 的导函数.
的导函数.
(1)若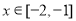 ,不等式
,不等式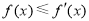 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(2)解关于x的方程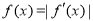 ;
;
(3)设函数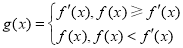 ,求
,求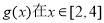 时的最小值.
时的最小值.
(1) ;(2)详见解析;(3)
;(2)详见解析;(3) .
.
【解析】
试题分析:本题主要考查导数的运算、利用导数求函数的最值、恒成立问题、分段函数、函数图象等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力,考查分类讨论思想. 第一问,先对 求导,得到
求导,得到 ,将
,将 ,不等式
,不等式 恒成立,转化为
恒成立,转化为 在
在 时恒成立,利用x的取值范围得到
时恒成立,利用x的取值范围得到 的最大值,从而得到a的取值范围;第二问,先得到
的最大值,从而得到a的取值范围;第二问,先得到 的方程,利用零点分段法去掉绝对值符号,通过对a的范围的讨论来解方程;第三问,先对
的方程,利用零点分段法去掉绝对值符号,通过对a的范围的讨论来解方程;第三问,先对
 中的1和
中的1和 的大小进行讨论,分别得到
的大小进行讨论,分别得到 的解析式,在每一种情况下利用一次函数、二次函数的图象及其性质得到函数的最小值.
的解析式,在每一种情况下利用一次函数、二次函数的图象及其性质得到函数的最小值.
试题解析:(1)∵ ,∴
,∴ , 1分
, 1分
又∵ ,知
,知
∴ 在
在 时恒成立,∵
时恒成立,∵ , 2分
, 2分
∴ . 3分
. 3分
⑵∵ ,∴
,∴ ,
,
∴ ,∴
,∴ 或
或 . 4分
. 4分
①当 时,
时, ,∴
,∴ 或
或
 ; 5分
; 5分
②当 时,
时, 或
或 ,
,
∴ 或
或
 或
或 ; 6分
; 6分
③当 时,
时, ,∴
,∴ 或
或 . 7分
. 7分
⑶∵ ,
,
①若 ,则
,则 时,
时, ,∴
,∴ ,
,
从而 的最小值为
的最小值为 ; 9分
; 9分
②若 ,则
,则 时,
时, ,∴
,∴ ,
,
当 时,
时, 的最小值为
的最小值为 ,
,
当 时,
时, 的最小值为
的最小值为 ,
,
当 时,
时, 的最小值为
的最小值为 . 11分
. 11分
③若 ,则
,则 时,
时,
当 时,
时, 最小值为
最小值为 ;
;
当 时,
时, 最小值为
最小值为 .
.
∵ ,
, ,
,
∴ 最小值为
最小值为 . 13分
. 13分
综上所述, 14分
14分
考点:导数的运算、利用导数求函数的最值、恒成立问题、分段函数、函数图象.

 是
是 上的单调函数,若函数
上的单调函数,若函数 只有一个零点,则实数
只有一个零点,则实数 的值是( )
的值是( ) B.
B. C.
C. D.
D.

 与直线
与直线  互相平行,则2a+3b的最小值为________.
互相平行,则2a+3b的最小值为________.
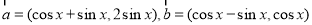 .令
.令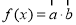 ,
,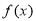 的最小正周期;
的最小正周期;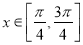 时,求
时,求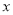 的值.
的值.
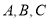 是平面内不共线的三点,点P在该平面内且有
是平面内不共线的三点,点P在该平面内且有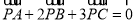 ,现将一粒黄豆随机撒在△
,现将一粒黄豆随机撒在△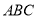 内,则这粒黄豆落在△
内,则这粒黄豆落在△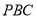 内的概率为__________.
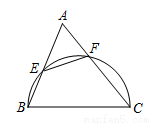
内的概率为__________.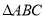 中,以
中,以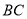 为直径的半圆分别交
为直径的半圆分别交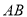 ,
,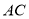 于点
于点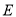 ,
,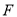 ,且
,且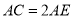 ,那么____;
,那么____; ___.
___.