题目内容
3.已知集合A={x|x2-2x-3>0},B={x|lg(x-2)≤1},则(∁RA)∪B=( )| A. | (-1,12) | B. | (2,3) | C. | (2,3] | D. | [-1,12] |
分析 首先化简集合A,B,进而算出∁RA,然后根据并集的定义进行求解.
解答 解:∵集合A={x|x2-2x-3>0}={x|x<-1或x>3}
∴∁RA={x|-1≤x≤3}=[-1,3]
∵B={x|lg(x-2)≤1},
∴$\left\{\begin{array}{l}{x-2>0}\\{x-2≤10}\end{array}\right.$,
解得2<x≤12,
∴B=(2,12]
∴(∁RA)∪B=[-1,12]
故选:D.
点评 此题主要考查了两个知识点补集的运算和并集的运算,是一道很基础的送分题,计算时认真即可.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
14.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,过点F1且垂直于x轴的直线与该双曲线的左支交于A、B两点,AF2、BF2分别交y轴于P、Q两点,若△PQF2的周长为12,则ab取得最大值时双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{3\sqrt{2}}{2}$ |
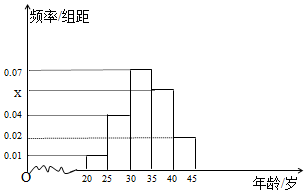 为响应国家“精准扶贫,产业扶贫”的战略,某市面向全市征召《扶贫政策》义务宣传志愿者,从年龄在[20,45]的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示.
为响应国家“精准扶贫,产业扶贫”的战略,某市面向全市征召《扶贫政策》义务宣传志愿者,从年龄在[20,45]的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示.