题目内容
14.函数y=2x-1的值域是( )| A. | (-∞,1) | B. | (-∞,0)∪(0,+∞) | C. | (-1,+∞) | D. | (-∞,-1)∪(0,+∞) |
分析 根据指数函数的值域可得函数y=2x-1的值域.
解答 解:∵y=2x的值域为(0,+∞),
那么:函数y=2x-1的值域为(-1,+∞).
故选:C.
点评 本题考查了函数值域的求法.高中函数值域求法有:1、观察法,2、配方法,3、反函数法,4、判别式法;5、换元法,6、数形结合法,7、不等式法,8、分离常数法,9、单调性法,10、利用导数求函数的值域,11、最值法,12、构造法,13、比例法.要根据题意选择.

练习册系列答案
相关题目
2.已知集合A={-1,0,1},B={x|x=sin$\frac{2k+1}{2}$π,k∈Z},则∁AB=( )
| A. | ? | B. | 0 | C. | {0} | D. | {-1,1} |
9.某三棱锥的三视图如图所示,该三棱锥的体积是( )
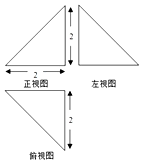

| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 4 | D. | $6+2\sqrt{3}$ |
19.已知集合A={x|x2-3x+2<0},B={x|y=lg(3-x)},则A∩B=( )
| A. | {x|1<x<2} | B. | {x|1<x<3} | C. | {x|2<x<3} | D. | {x|x<3} |
6.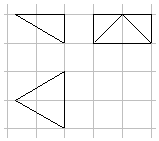 如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,已知其俯视图是正三角形,则该四棱锥的外接球的表面积是( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,已知其俯视图是正三角形,则该四棱锥的外接球的表面积是( )
 如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,已知其俯视图是正三角形,则该四棱锥的外接球的表面积是( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,已知其俯视图是正三角形,则该四棱锥的外接球的表面积是( )| A. | $\frac{19π}{3}$ | B. | $\frac{22π}{3}$ | C. | 19π | D. | 22π |
3.近年来,我国电子商务蓬勃发展.2016年“618”期间,某网购平台的销售业绩高达516亿元人民币,与此同时,相关管理部门推出了针对该网购平台的商品和服务的评价系统.从该评价系统中选出200次成功交易,并对其评价进行统计,网购者对商品的满意率为0.6,对服务的满意率为0.75,其中对商品和服务都满意的交易为80次.
(Ⅰ) 根据已知条件完成下面的2×2列联表,并回答能否有99%的把握认为“网购者对商品满意与对服务满意之间有关系”?
(Ⅱ) 若将频率视为概率,某人在该网购平台上进行的3次购物中,设对商品和服务都满
意的次数为随机变量X,求X的分布列和数学期望EX.
附:K2=$\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$(其中n=a+b+c+d为样本容量)
(Ⅰ) 根据已知条件完成下面的2×2列联表,并回答能否有99%的把握认为“网购者对商品满意与对服务满意之间有关系”?
| 对服务满意 | 对服务不满意 | 合计 | |
| 对商品满意 | 80 | ||
| 对商品不满意 | |||
| 合计 | 200 |
意的次数为随机变量X,求X的分布列和数学期望EX.
附:K2=$\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$(其中n=a+b+c+d为样本容量)
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
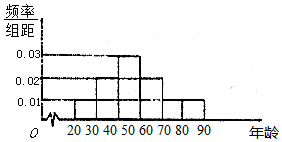 退休年龄延迟是平均预期寿命延长和人口老龄化背景下的一种趋势,某机构为了解某城市市民的年龄构成,从该城市市民中随机抽取年龄段在20~80岁(含20岁和80岁)之间的600人进行调查,并按年龄层次绘制频率分布直方图,如图所示,若规定年龄分布在60~80岁(含60岁和80岁)为“老年人”.
退休年龄延迟是平均预期寿命延长和人口老龄化背景下的一种趋势,某机构为了解某城市市民的年龄构成,从该城市市民中随机抽取年龄段在20~80岁(含20岁和80岁)之间的600人进行调查,并按年龄层次绘制频率分布直方图,如图所示,若规定年龄分布在60~80岁(含60岁和80岁)为“老年人”.