题目内容
13.已知a>0,且a≠1,解关于x的不等式2loga(x-3)>logax2.分析 由已知不等式分a>1和0<a<1转化为关于x的不等式组求解,最后取并集得答案.
解答 解:(1)当a>1时,不等式2loga(x-3)>logax2?$\left\{\begin{array}{l}{x-3>0}\\{{x}^{2}>0}\\{(x-3)^{2}>{x}^{2}}\end{array}\right.$,解得x∈∅;
(2)当0<a<1时,不等式2loga(x-3)>logax2?$\left\{\begin{array}{l}{x-3>0}\\{{x}^{2}>0}\\{(x-3)^{2}<{x}^{2}}\end{array}\right.$,解得x>3;
综上可知,当a>1时,不等式的解集为∅;当0<a<1时,不等式的解集为{x|x>3}.
点评 本题考查对数不等式的解法,考查了分类讨论的数学思想方法,是中档题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
2.已知数列{an}的通项公式为an=3n-50,则当n等于( )时,Sn取得最小值?
| A. | 16 | B. | 17 | C. | 18 | D. | 16或17 |
3.下列是x和y之间的一组数据
则y关于x的线性回归方程为y=bx+a,对应的直线必过点( )
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
| A. | (2,2) | B. | ($\frac{3}{2},2$) | C. | ( $\frac{3}{2},4$) | D. | (1,2) |
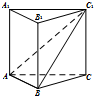 如图,三棱柱ABC-A1B1C1的各条棱长均为2,且侧棱垂直于底面,则二面角C1-AB-C的正切值为$\frac{2\sqrt{3}}{3}$.
如图,三棱柱ABC-A1B1C1的各条棱长均为2,且侧棱垂直于底面,则二面角C1-AB-C的正切值为$\frac{2\sqrt{3}}{3}$.