题目内容
20.已知$\sqrt{3}$sin(π-x)+cos(-x)=$\frac{8}{5}$,则cos(x-$\frac{π}{3}$)=( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{7}{5}$ |
分析 利用诱导公式化简已知可得$\frac{\sqrt{3}}{2}$sinx+$\frac{1}{2}$cosx=$\frac{4}{5}$,利用两角差的余弦函数公式化简所求即可计算得解.
解答 解:∵$\sqrt{3}$sin(π-x)+cos(-x)=$\frac{8}{5}$,
⇒$\sqrt{3}$sinx+cosx=$\frac{8}{5}$,
⇒2($\frac{\sqrt{3}}{2}$sinx+$\frac{1}{2}$cosx)=$\frac{8}{5}$,
⇒$\frac{\sqrt{3}}{2}$sinx+$\frac{1}{2}$cosx=$\frac{4}{5}$,
∴cos(x-$\frac{π}{3}$)=$\frac{1}{2}$cosx+$\frac{\sqrt{3}}{2}$sinx=$\frac{4}{5}$.
故选:B.
点评 本题主要考查了诱导公式,两角差的余弦函数公式在三角函数化简求值中的应用,属于基础题.

练习册系列答案
相关题目
8.已知向量|$\overrightarrow{a}$|=$\sqrt{3}$,|$\overrightarrow{b}$|=$\sqrt{6}$,若$\overrightarrow{a}$,$\overrightarrow{b}$间的夹角为$\frac{3π}{4}$,则|4$\overrightarrow{a}$-$\overrightarrow{b}$|=( )
| A. | $\sqrt{57}$ | B. | $\sqrt{61}$ | C. | $\sqrt{78}$ | D. | $\sqrt{85}$ |
15.设函数y=ax2与函数y=|$\frac{lnx+1}{ax}$|的图象恰有3个不同的交点,则实数a的取值范围为( )
| A. | ($\frac{\sqrt{3}}{3}$e,$\sqrt{e}$) | B. | (-$\frac{\sqrt{3}}{3}$e,0)∪(0,$\frac{\sqrt{3}}{3}$e) | C. | (0,$\frac{\sqrt{3}}{3}$e) | D. | ($\frac{1}{\sqrt{e}}$,1)∪{$\frac{\sqrt{3}}{3}$e} |
12.已知α、β是两个不同的平面,m、n是两条不同的直线,下列命题中正确的是( )
| A. | 若α∥β,m⊥n,m⊥α,则n∥β | B. | 若α⊥β,m∥n,m⊥β,则n?α | ||
| C. | 若n⊥α,m⊥α,则m∥n | D. | 若α⊥β,n∥α,m⊥β,则m⊥n |
9.已知全集U={1,2,3,4,5},集合M={1,2,3},N={3,4,5},则集合{1,2}可以表示为( )
| A. | M∩N | B. | (∁UM)∩N | C. | M∩(∁UN) | D. | (∁UM)∩(∁UN) |
10.设p:1<x<2,q:lnx<1,则p是q成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 即不充分也不必要条件 |
 如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体外接球的表面积为$\frac{41π}{4}$.
如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体外接球的表面积为$\frac{41π}{4}$.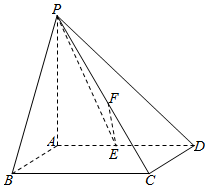 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是正方形,且PA=AD=2,E,F分别是棱AD,PC的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是正方形,且PA=AD=2,E,F分别是棱AD,PC的中点.