题目内容
16.化简$\overrightarrow{AC}+\overrightarrow{DB}+\overrightarrow{CD}$=$\overrightarrow{AB}$.分析 根据向量的线性运算的性质判断即可.
解答 解:$\overrightarrow{AC}+\overrightarrow{DB}+\overrightarrow{CD}$=$\overrightarrow{AC}$+$\overrightarrow{CD}$+$\overrightarrow{DB}$=$\overrightarrow{AD}$+$\overrightarrow{DB}$=$\overrightarrow{AB}$,
故答案为:$\overrightarrow{AB}$.
点评 本题考查了向量的线性运算,是一道基础题.

练习册系列答案
相关题目
6.若$sinα=\frac{3}{5}(0<α<\frac{π}{2})$,则$sin(α+\frac{π}{6})$=( )
| A. | $\frac{{3\sqrt{3}-4}}{10}$ | B. | $\frac{{3\sqrt{3}+4}}{10}$ | C. | $\frac{{3-4\sqrt{3}}}{10}$ | D. | $\frac{{3+4\sqrt{3}}}{10}$ |
7.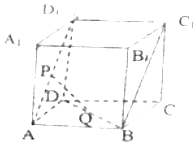 如图,点P、Q分别是正方体ABCD-A1B1C1D1的面对角线AD1、BD的中点,则异面直线PQ和BC1所成的角为( )
如图,点P、Q分别是正方体ABCD-A1B1C1D1的面对角线AD1、BD的中点,则异面直线PQ和BC1所成的角为( )
 如图,点P、Q分别是正方体ABCD-A1B1C1D1的面对角线AD1、BD的中点,则异面直线PQ和BC1所成的角为( )
如图,点P、Q分别是正方体ABCD-A1B1C1D1的面对角线AD1、BD的中点,则异面直线PQ和BC1所成的角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
4.函数f(x)对任意实数x都满足条件f(x+2)f(x)=1,若f(2)=2,则f(2016)=( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{2016}$ | D. | 2016 |
1.命题“存在x0∈R,log2x0<0”的否定是( )
| A. | 对任意的x∈R,log2x<0 | B. | 对任意的x∈R,log2x≥0 | ||
| C. | 不存在x∈R,log2x≥0 | D. | 存在x0∈R,log2x0≥0 |
5.函数y=Asin(ωx+φ)(ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,则函数的一个表达式为( )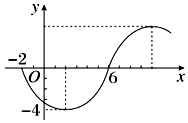

| A. | y=-4sin($\frac{π}{8}$x+$\frac{π}{4}$) | B. | y=4sin($\frac{π}{8}$x-$\frac{π}{4}$) | C. | y=-4sin($\frac{π}{8}$x-$\frac{π}{4}$) | D. | y=4sin($\frac{π}{8}$x+$\frac{π}{4}$) |
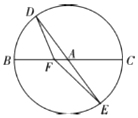 如图,BC是单位圆A的一条直径,F是线段AB上的点,且$\overrightarrow{BF}$=3$\overrightarrow{FA}$,若DE是圆A中绕圆心A运动的一条直径,则$\overrightarrow{FD}$•$\overrightarrow{FE}$的值是$-\frac{15}{16}$.
如图,BC是单位圆A的一条直径,F是线段AB上的点,且$\overrightarrow{BF}$=3$\overrightarrow{FA}$,若DE是圆A中绕圆心A运动的一条直径,则$\overrightarrow{FD}$•$\overrightarrow{FE}$的值是$-\frac{15}{16}$.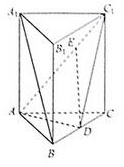 在正三棱柱ABC-A1B1C1中,点D为BC的中点;
在正三棱柱ABC-A1B1C1中,点D为BC的中点;