题目内容
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π,在一周期内,当x=
时,y取得最大值3,当x=
时,y取得最小值-3,求:
(1)函数的解析式;
(2)求出函数f(x)的单调递增区间与对称轴方程,对称中心坐标;
(3)当x∈[-
,
]时,求函数f(x)的值域.
| π |
| 12 |
| 7π |
| 12 |
(1)函数的解析式;
(2)求出函数f(x)的单调递增区间与对称轴方程,对称中心坐标;
(3)当x∈[-
| π |
| 12 |
| π |
| 6 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的单调性,正弦函数的对称性
专题:计算题,三角函数的图像与性质
分析:(1)根据函数在一个周期内的最大、最小值及相应的x值,可得A=3且ω=2,再由函数在x=
时取得最小值-3,列式解出φ=
,由此得到函数的表达式.
(2)根据三角函数单调区间和对称轴方程的结论,可得函数的单调增区间和对称轴方程,对称中心坐标;
(3)当x∈[-
,
]时,可得2x+
∈[
,
],结合三角函数的图象与性质即可得到函数f(x)的值域.
| 7π |
| 12 |
| π |
| 3 |
(2)根据三角函数单调区间和对称轴方程的结论,可得函数的单调增区间和对称轴方程,对称中心坐标;
(3)当x∈[-
| π |
| 12 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
解答:
解:(1)∵在一周期内,函数当x=
时取得最大值3,当x=
时取得最小值-3.
∴正数A=3,周期T满足
=
-
=
,得T=π,∴ω=
=2
因此,函数表达式为f(x)=3sin(2x+φ),
将点(
,-3)代入,得-3=3sin(2×
+φ),即sin(2×
+φ)=-1
∴
+φ=-
+2mπ,m∈Z
∵|φ|<π,∴取m=1,得φ=
综上所述,f(x)的解析式为f(x)=3sin(2x+
)
(2)令-
+2kπ<2x+
<
+2kπ,解得-
+kπ<x<
+kπ,k∈Z
∴函数f(x) 的单调增区间为(-
+kπ,
+kπ),k∈Z
由2x+
=
+kπ,解得x=
+
,k∈Z
∴函数图象的对称轴方程为x=
+
,k∈Z.
由2x+
=kπ,解得x=
-
,k∈Z
∴函数f(x)的对称中心坐标为(
-
,0)(k∈Z);
(3)∵x∈[-
,
],
∴2x+
∈[
,
],可得
≤sin(2x+
)≤
即得
≤3sin(2x+
)≤
因此,函数f(x)=3sin(2x+
)的值域为[
,
].
| π |
| 12 |
| 7π |
| 12 |
∴正数A=3,周期T满足
| T |
| 2 |
| 7π |
| 12 |
| π |
| 12 |
| π |
| 2 |
| 2π |
| T |
因此,函数表达式为f(x)=3sin(2x+φ),
将点(
| 7π |
| 12 |
| 7π |
| 12 |
| 7π |
| 12 |
∴
| 7π |
| 6 |
| π |
| 2 |
∵|φ|<π,∴取m=1,得φ=
| π |
| 3 |
综上所述,f(x)的解析式为f(x)=3sin(2x+
| π |
| 3 |
(2)令-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
| π |
| 12 |
∴函数f(x) 的单调增区间为(-
| 5π |
| 12 |
| π |
| 12 |
由2x+
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
| kπ |
| 2 |
∴函数图象的对称轴方程为x=
| π |
| 12 |
| kπ |
| 2 |
由2x+
| π |
| 3 |
| kπ |
| 2 |
| π |
| 6 |
∴函数f(x)的对称中心坐标为(
| kπ |
| 2 |
| π |
| 6 |
(3)∵x∈[-
| π |
| 12 |
| π |
| 6 |
∴2x+
| π |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| ||
| 2 |
即得
| 3 |
| 2 |
| π |
| 3 |
3
| ||
| 2 |
因此,函数f(x)=3sin(2x+
| π |
| 3 |
| 3 |
| 2 |
3
| ||
| 2 |
点评:本题给出三角函数式满足的条件,求函数f(x)的单调区间和闭区间上的值域,着重考查了由y=Asin(ωx+φ)的部分图象确定其解析式等知识、正弦函数的图象与性质等知识,属于中档题.

练习册系列答案
相关题目
若二项式(
+
)n展开式中存在常数项,则n的必须是( )
| x |
| 2 | |||
|
| A、3的倍数 | B、4的倍数 |
| C、5的倍数 | D、6的倍数 |
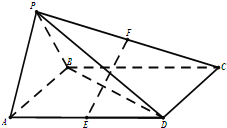 四棱锥P-ABCD底面是平行四边形,平面PAB⊥平面ABCD,PA=PB=AB=
四棱锥P-ABCD底面是平行四边形,平面PAB⊥平面ABCD,PA=PB=AB=