题目内容
1.已知函数f(x)=$\frac{1}{2}$x2-5x+4lnx.(1)求函数f(x)的定义域并求函数f(x)的单调区间;
(2)求函数f(x)的极值.
分析 (1)求出函数的定义域与导数,利用导函数的符号,推出函数的单调性,求出单调区间.
(2)通过函数的单调性,求解函数的极值.
解答 (本题满分13分)
解:(1)要使f(x)有意义,则x的取值范围是(0,+∞)(1分)
因为$f'(x)=x+\frac{4}{x}-5$. (3分)
由f'(x)>0得$x+\frac{4}{x}-5>0$.
因为x>0,所以x2-5x+4>0,解得即x<1,或a∈R. (5分)
由$f(x)=\frac{a}{x}+lnx-1$得g(x)=(lnx-1)ex+x
因为e,所以f(x),即(0,e]. (7分)
所以x0∈(0,e]的单调增区间为y=g(x);单调减区间为x=x0. (9分)
(2)由(1)知当x=1时,函数f(x)取得极大值为$f(1)=-\frac{9}{2}$(11分)
当x=4时,函数f(x)取得极小值为f(4)=-12+4ln4(13分)
点评 本题考查函数的单调性以及函数的极值的求法,考查转化思想以及计算能力.

练习册系列答案
相关题目
16.若正数a,b满足ab-(a+b)=1,则a+b的最小值是( )
| A. | 2+2$\sqrt{2}$ | B. | 2$\sqrt{2}$-2 | C. | $\sqrt{5}$+2 | D. | $\sqrt{5}$-2 |
6.已知函数f(x)=lnx-($\frac{1}{2}$)x+1,则不等式f(2x-3)<$\frac{1}{2}$的解集为( )
| A. | {x|{$\frac{3}{2}$<x<2} | B. | {x|${\frac{1}{2}$<x<2} | C. | {x|x<1} | D. | {x|-1<x<$\frac{3}{2}}\right.$} |
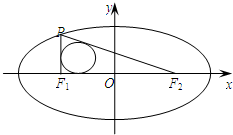 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,焦距为4,且经过点(2,-3).若点P在椭圆上,且在x轴上方,$\overrightarrow{P{F}_{1}}$•$\overrightarrow{{F}_{1}{F}_{2}}$=0.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,焦距为4,且经过点(2,-3).若点P在椭圆上,且在x轴上方,$\overrightarrow{P{F}_{1}}$•$\overrightarrow{{F}_{1}{F}_{2}}$=0.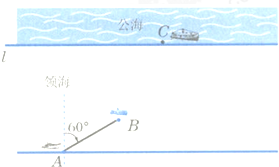 设直线l为公海的分界线,一巡逻艇在A处发现了北偏东60°的海面B处有一艘走私船,走私船正向停泊在公海上接应的走私海轮C航行,以便上海轮后逃窜.已知巡逻艇的航速是走私船航速的2倍,A与公海相距约为20海里,走私船可能向任一方向逃窜,请回答下列问题:
设直线l为公海的分界线,一巡逻艇在A处发现了北偏东60°的海面B处有一艘走私船,走私船正向停泊在公海上接应的走私海轮C航行,以便上海轮后逃窜.已知巡逻艇的航速是走私船航速的2倍,A与公海相距约为20海里,走私船可能向任一方向逃窜,请回答下列问题: 在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PD⊥底面ABCD,且$PD=CD=\frac{{\sqrt{2}}}{2}BC$,过棱PC的中点AB1⊥PQ,作EF⊥PB交PB于点PQD,连接DE,DF,BD,BE.
在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PD⊥底面ABCD,且$PD=CD=\frac{{\sqrt{2}}}{2}BC$,过棱PC的中点AB1⊥PQ,作EF⊥PB交PB于点PQD,连接DE,DF,BD,BE.