题目内容
已知函数fn(x)=
+
+
…+
+
(x+1),其中n∈N*,当n=1,2,3,…时,fn(x)的零点依次记作x1,x2,x3,…,则
xn= .
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| n(n+1) |
| 2015n+2n+1 |
| 2n+2015n+1 |
| lim |
| n→∞ |
考点:数列的极限
专题:计算题,等差数列与等比数列
分析:利用裂项法求和,令fn(x)=0,解得xn=
•
-1,利用极限的运算法则即可得出.
| n |
| n+1 |
(
| ||
2•(
|
解答:
解:函数fn(x)=
+
+
…+
+
(x+1)=1-
+
(x+1),
令fn(x)=0,解得xn=
•
-1.
∴
xn=1×2015-1=2014.
故答案为:2014.
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| n(n+1) |
| 2015n+2n+1 |
| 2n+2015n+1 |
| 1 |
| n+1 |
| 2015n+2n+1 |
| 2n+2015n+1 |
令fn(x)=0,解得xn=
| n |
| n+1 |
(
| ||
2•(
|
∴
| lim |
| n→∞ |
故答案为:2014.
点评:本题考查了裂项法求和、数列极限的运算法则,属于基础题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
某流程图如图所示,现输入如下四个函数,则可以输出的函数是( )
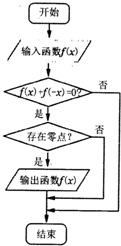

A、f(x)=
| ||||||
B、f(x)=
| ||||||
C、f(x)=
| ||||||
| D、f(x)=x2ln(x2+1) |
已知直线y=2x为双曲线Γ:
-
=1(a>0,b>0)的一条渐近线,则双曲线Γ的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|