题目内容

17．已知函数f（x）=x2-|x|+a-1有四个零点，则a的取值范围是$（\;1\;，\;\frac{5}{4}\;）$．

分析 将方程的零点问题转化成函数的交点问题，作出函数的图象得到a的范围．

解答 解：由f（x）=x2-|x|+a-1=0，
得a-1=-x2+|x|，
作出y=-x2+|x|与y=a-1的图象，

要使函数f（x）=x2-|x|+a-1有四个零点，
则y=-x2+|x|与y=a-1的图象有四个不同的交点，
所以0＜a-1＜$\frac{1}{4}$，
解得：a∈$（\;1\;，\;\frac{5}{4}\;）$
故答案为：$（\;1\;，\;\frac{5}{4}\;）$

点评 本题考查等价转化的能力、利用数形结合解题的数学思想方法是重点，属中档题．

练习册系列答案
相关题目
7．已知圆C：x2+（y-1）2=5，直线l：mx-y+1-m=0，且直线与圆C交于A，B两点，若点P（1，1）满足2$\overrightarrow{AP}$=$\overrightarrow{PB}$，则直线l的方程为x-y=0或x+y-2=0．
8．“莫以宜春远，江山多胜游”，近年来，宜春市在旅游业方面抓品牌创建，推进养生休闲度假旅游产品升级，明月山景区成功创建国家5A级旅游景区填补了赣西片区的空白，某投资人看到宜春旅游发展的大好前景后，打算在宜春投资甲，乙两个旅游项目，根据市场前期调查，甲，乙两个旅游项目五年后可能的最大盈利率分别为100%和80%，可能的最大亏损率分别为40%和20%，投资人计划投资金额不超过5000万，要求确保亏损不超过1200万，问投资人对两个项目各投资多少万元，才能使五年后可能的盈利最大？
5．某商场举行有奖促销活动，顾客购买一定金额的商品后即可参加抽奖，抽奖有两种方案可供选择．
方案一：从装有4个红球和2个白球的不透明箱中，随机摸出2个球，若摸出的2个球都是红球则中奖，否则不中奖；
方案二：掷2颗骰子，如果出现的点数至少有一个为4则中奖，否则不中奖．（注：骰子（或球）的大小、形状、质地均相同）
（Ⅰ）有顾客认为，在方案一种，箱子中的红球个数比白球个数多，所以中奖的概率大于$\frac{1}{2}$．你认为正确吗？请说明理由；
（Ⅱ）如果是你参加抽奖，你会选择哪种方案？请说明理由．
12．有一个几何体的三视图如图所示，这个几何体应是一个（　　）
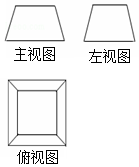
A．棱台B．棱锥C．棱柱D．正四面体
2．已知焦点在x 轴上的双曲线的渐近线方程为$y=±\frac{1}{2}x$，则双曲线的离心率为（　　）
A．$\frac{5}{4}$B．$\frac{{\sqrt{5}}}{2}$C．$\frac{{\sqrt{3}}}{2}$D．2
9．珠海市板樟山森林公园（又称澳门回归公园）的山顶平台上，有一座百子回归碑．百子回归碑是一座百年澳门简史，记载着近年来澳门的重大历史事件以及有关史地，人文资料等，如中央四数连读为1999-12-20标示澳门回归日，中央靠下有23-50标示澳门面积约为23.50 平方公里．百子回归碑实为一个十阶幻方，是由1 到100 共100 个整数填满100个空格，其横行数字之和与直列数字之和以及对角线数字之和都相等．请问如图2 中对角线上数字（从左上到右下）之和为505．
6．已知集合M={x|x＞2}，$a=\sqrt{5}$，则下列关系式正确的是（　　）
A．a⊆MB．a∉MC．{a}∉MD．{a}⊆M
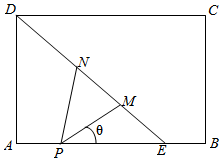7．如图，矩形ABCD是一个历史文物展览厅的俯视图，点E在AB上，在梯形BCDE区域内部展示文物，DE是玻璃幕墙，游客只能在△ADE区域内参观，在AE上点P处安装一可旋转的监控摄像头，∠MPN为监控角，其中M、N在线段DE（含端点）上，且点M在点N的右下方，经测量得知：AD=6米，AE=6米，AP=2米，∠MPN=$\frac{π}{4}$，记∠EPM=θ（弧度），监控摄像头的可视区域△PMN的面积为S平方米．
（1）求S关于θ的函数关系式，并写出θ的取值范围：（参考数据：tan$\frac{5}{4}$≈3）
2）求S的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网