题目内容
4.填空:(1)${C}_{3n}^{38-n}{+C}_{21+n}^{3n}$=466;
(2)${C}_{13+n}^{3n}{+C}_{12+n}^{3n-1}{+C}_{11+n}^{3n-2}+…{+C}_{2n}^{17-n}$=124;
(3)${C}_{3}^{3}{+C}_{4}^{3}{+C}_{5}^{3}+…{+C}_{10}^{3}$=330.
分析 (1)根据组合数的意义,求出n=20,再计算${C}_{3n}^{38-n}{+C}_{21+n}^{3n}$的值;
(2)根据组合数的意义,求出n=6,再代人计算${C}_{13+n}^{3n}{+C}_{12+n}^{3n-1}{+C}_{11+n}^{3n-2}+…{+C}_{2n}^{17-n}$的值;
(3)根据组合数公式${C}_{n}^{m}$+${C}_{n}^{m-1}$=${C}_{n+1}^{m}$,进行化简与运算即可.
解答 解:(1)∵$\left\{\begin{array}{l}{3n≥38-n}\\{3n≤21+n}\end{array}\right.$,
∴$\frac{19}{2}$≤n≤$\frac{21}{2}$,
又∵n∈N*,
∴n=20,
即${C}_{3n}^{38-n}{+C}_{21+n}^{3n}$=${C}_{30}^{28}$+${C}_{31}^{30}$
=${C}_{30}^{2}$+${C}_{31}^{1}$
=$\frac{30×29}{2}$+31
=466;
(2)∵$\left\{\begin{array}{l}{3n≤13+n}\\{2n≥17-n}\end{array}\right.$,
∴$\frac{17}{3}$≤n≤$\frac{13}{2}$,
又∵n∈N*,
∴n=6;
∴${C}_{13+n}^{3n}{+C}_{12+n}^{3n-1}{+C}_{11+n}^{3n-2}+…{+C}_{2n}^{17-n}$
=${C}_{19}^{18}$+${C}_{18}^{17}$+${C}_{17}^{16}$+…+${C}_{12}^{11}$
=${C}_{19}^{1}$+${C}_{18}^{1}$+${C}_{17}^{1}$+…+${C}_{12}^{1}$
=19+18+17+…+12
=$\frac{(19+12)×8}{2}$=124;
(3)${C}_{3}^{3}{+C}_{4}^{3}{+C}_{5}^{3}+…{+C}_{10}^{3}$=${C}_{4}^{4}$+${C}_{4}^{3}$+${C}_{5}^{3}$+…+${C}_{10}^{3}$
=${C}_{5}^{4}$+${C}_{5}^{3}$+…+${C}_{10}^{3}$
=${C}_{6}^{4}$+…+${C}_{10}^{3}$
=…=${C}_{10}^{4}$+${C}_{10}^{3}$=${C}_{11}^{4}$=330.
故答案为:466,124,330.
点评 本题考查了组合数公式的定义与性质的意义问题,也考查了转化思想与计算能力,是基础题目.

| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
| A. | 2$\sqrt{3}$ | B. | 2$\sqrt{5}$ | C. | 2$\sqrt{10}$ | D. | 2$\sqrt{15}$ |
| A. | 关于原点对称 | B. | 关于直线y=x对称 | C. | 关于x轴对称 | D. | 关于y轴对称 |
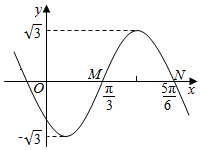 如图为函数y=f(x)=Asin(wx+φ)(A>3,w>0,|φ|<π)图象的一部分.
如图为函数y=f(x)=Asin(wx+φ)(A>3,w>0,|φ|<π)图象的一部分.