题目内容
已知向量
、
满足|
|=
,|
-
|=
,(
,
)=
,则|
|等于( )
| a |
| b |
| a |
| 2 |
| a |
| b |
| 5 |
| a |
| b |
| π |
| 4 |
| b |
| A、2 | ||
B、
| ||
| C、3 | ||
D、2
|
考点:平面向量数量积的运算
专题:平面向量及应用
分析:利用向量的数量积运算性质及其定义即可得出.
解答:
解:∵向量
、
满足|
|=
,|
-
|=
,<
,
>=
,
∴
=
,
∴2+|
|2-2×
|
|cos
=5,
化为|
|2-2|
|-3=0,
解得|
|=3.
故选:C.
| a |
| b |
| a |
| 2 |
| a |
| b |
| 5 |
| a |
| b |
| π |
| 4 |
∴
|
| 5 |
∴2+|
| b |
| 2 |
| b |
| π |
| 4 |
化为|
| b |
| b |
解得|
| b |
故选:C.
点评:本题考查了向量的数量积运算性质及其定义,属于基础题.

练习册系列答案
相关题目
函数y=x2+x的递增区间是( )
| A、(0,+∞) | ||
| B、(-∞,1) | ||
C、(
| ||
| D、(1,+∞) |
已知函数f(x)=4sin2x+2sin2x-2,(0°<x<90°),当f(x)取最大值时的x=( )
| A、15° | B、22.5° |
| C、37.5° | D、67.5° |
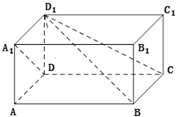 在四棱柱ABCD-A1B1C1D1中,底面ABCD是矩形,侧棱DD1⊥平面ABCD,且AD=AA1=1,AB=2.
在四棱柱ABCD-A1B1C1D1中,底面ABCD是矩形,侧棱DD1⊥平面ABCD,且AD=AA1=1,AB=2. 如图,正四棱柱ABCD-A1B1C1D1的底面边长为2,高为4,那么异面直线BD1与AD所成角的正切值( )
如图,正四棱柱ABCD-A1B1C1D1的底面边长为2,高为4,那么异面直线BD1与AD所成角的正切值( )