题目内容
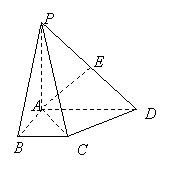
如图,在四棱锥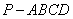 中,
中,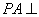 平面
平面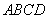 ,底面
,底面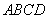 是直角梯形,
是直角梯形,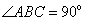 ,
, ∥
∥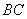 ,且
,且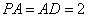 ,
,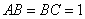 ,
, 为
为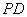 的中点.
的中点.
(Ⅰ)设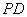 与平面
与平面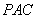 所成的角为
所成的角为 ,二面角
,二面角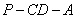 的
的
大小为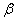 ,求证:
,求证: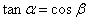 ;
;
(Ⅱ)在线段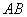 上是否存在一点
上是否存在一点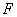 (与
(与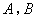 两点不重合),使得
两点不重合),使得
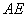 ∥平面
∥平面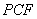 ? 若存在,求
? 若存在,求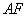 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
解法一:(1)证明: 又
又


又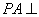 平面
平面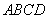 ,
, ,
, 面
面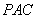
∴

 ,
,

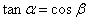
(2) 取 的中点
的中点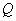 ,连
,连 交
交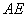 于
于 ,由
,由 与
与 相似得,
相似得, ,
,
在 上取点
上取点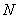 ,使
,使 ,则
,则 ,
,
在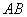 上取点
上取点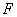 使
使 ,由于
,由于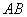 平行且等于
平行且等于 ,
,
故有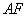 平行且等于
平行且等于 ,
,
四边形 为平行四边形,所以
为平行四边形,所以 ,
,
而 , 故有
, 故有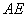 ∥平面
∥平面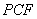 ,
,
所以在线段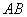 上存在一点
上存在一点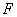 使得
使得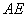 ∥平面
∥平面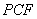 ,
,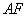 的长为
的长为 .
.
解法二:(1)同解法一;
(2)如图,以 为原点,
为原点, 所在直线分别为
所在直线分别为 轴,建立直角坐标系,则
轴,建立直角坐标系,则 ,
, 为
为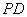 的中点,则
的中点,则
假设存在符合条件的点 ,则
,则 共面,
共面,
故存在实数 ,使得
,使得

即 ,故有
,故有 即
即
即存在符合条件的点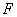 ,
,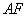 的长为
的长为 .
.

练习册系列答案
相关题目
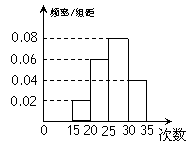

 在(0,+
在(0,+ )内有定义,对于给定的正数K,定义函数
)内有定义,对于给定的正数K,定义函数 ,取函数
,取函数 ,恒有
,恒有 ,则
,则 B.K的最小值为
B.K的最小值为 为坐标原点,
为坐标原点, 两点的坐标均满足不等式组
两点的坐标均满足不等式组 设
设 与
与 的夹角为
的夹角为 ,则
,则 的最大值为
的最大值为  B.
B. C.
C. D.
D.
 的线段分成
的线段分成 段,每段长度均为正整数,并要求这
段,每段长度均为正整数,并要求这 段中的任意三段都不能构成三角形.例如,当
段中的任意三段都不能构成三角形.例如,当 时,只可以分为长度分别为1,1,2的三段,此时
时,只可以分为长度分别为1,1,2的三段,此时 时,可以分为长度分别为1,2,4的三段或长度分别为1,1,2,3的四段,此时
时,可以分为长度分别为1,2,4的三段或长度分别为1,1,2,3的四段,此时 时,
时, 时,
时, 为虚数单位,
为虚数单位, ,则
,则 ( )
( ) C.
C.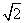 D.1
D.1 ,若关于
,若关于 的方程
的方程 有两个不同的实根,则实数
有两个不同的实根,则实数 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 在点
在点 处的切线方程为( )
处的切线方程为( ) B.
B.
 D.
D.
 +cos2x-sin2x.
+cos2x-sin2x. π,
π, π]的图像(只作图不写过程).
π]的图像(只作图不写过程).