题目内容
已知函数f(x)= +cos2x-sin2x.
+cos2x-sin2x.
(1)求函数f(x)的最小正周期和单调递减区间;
(2)在所给坐标系中画出函数在区间[ π,
π, π]的图像(只作图不写过程).
π]的图像(只作图不写过程).

解:f(x)= +cos 2x=sin 2x+cos 2x=
+cos 2x=sin 2x+cos 2x= sin(2x+
sin(2x+ ).
).
(1)函数f(x)的最小正周期T= =π,令2kπ+
=π,令2kπ+ ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ π,k∈Z,
π,k∈Z,
则2kπ+ ≤2x≤2kπ+
≤2x≤2kπ+ π,k∈Z,故kπ+
π,k∈Z,故kπ+ ≤x≤kπ+
≤x≤kπ+ π,k∈Z.
π,k∈Z.
所以函数f(x)的单调递减区间为[kπ+ ,kπ+
,kπ+ π](k∈Z).
π](k∈Z).
(2)图像如下:
 |

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
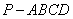 中,
中,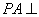 平面
平面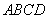 ,底面
,底面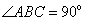 ,
, ∥
∥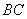 ,且
,且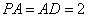 ,
,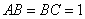 ,
, 为
为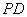 的中点.
的中点.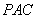 所成的角为
所成的角为 ,二面角
,二面角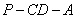 的
的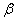 ,求证:
,求证: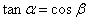 ;
;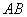 上是否存在一点
上是否存在一点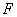 (与
(与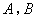 两点不重合),使得
两点不重合),使得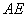 ∥平面
∥平面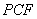 ? 若存在,求
? 若存在,求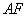 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.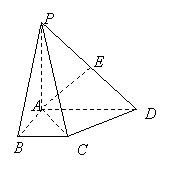
 在点
在点 处的切线与坐标轴所围三角形的面积为____ ____.
处的切线与坐标轴所围三角形的面积为____ ____. ,且tanα<0,则sin2α的值等于 ( )
,且tanα<0,则sin2α的值等于 ( )  B.
B. C.-
C.- 与函数
与函数 和
和 的图象分别交于
的图象分别交于 、
、 两点,则
两点,则 的最大值为____.
的最大值为____. 的高,从山脚
的高,从山脚 测得
测得 m, 塔顶
m, 塔顶 的仰角
的仰角 ,塔底
,塔底 的仰角
的仰角 ,则井架的高
,则井架的高 A.
A. m B.
m B. m C.
m C. m D.
m D. m
m
 在
在 方向上的投影为
方向上的投影为  的部分图象如图所示,则
的部分图象如图所示,则 和
和 的值可以是 ( )
的值可以是 ( ) (A)
(A) (B)
(B)
 (D)
(D)
 =2
=2 .
. (t∈R为参数),求a,b的值.
(t∈R为参数),求a,b的值.