题目内容
等差数列{an}中,a3+a13=-8,数列{bn}是等比数列,若b7=a8,则b6•b8的值为( )
| A、2 | B、4 | C、8 | D、16 |
考点:等差数列的性质
专题:计算题,等差数列与等比数列
分析:由等差数列的性质结合已知条件求得a8,则b7可求,再由等比数列的性质求得b6•b8的值.
解答:
解:在等差数列{an}中,
∵a3+a13=-8,
由等差数列的性质得:2a8=a3+a13=-8,
∴a8=-4.
则b7=a8=-4.
∴在等比数列{bn}中,b6•b8=b72=16.
故选:D.
∵a3+a13=-8,
由等差数列的性质得:2a8=a3+a13=-8,
∴a8=-4.
则b7=a8=-4.
∴在等比数列{bn}中,b6•b8=b72=16.
故选:D.
点评:本题考查了等差数列和等比数列的性质,是基础的计算题.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
已知集合M={x|y=
,x∈Z},N={y|y=3x+1,x∈R},则M∩N的真子集个数为( )
| 4-x2 |
| A、5 | B、7 | C、31 | D、3 |
中心点在原点,准线方程为x=±4,离心率为
的椭圆方程是( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、x2+
|
等差数列{an}中,a3=5,a5=9,则这个等差数列的公差为( )
| A、4 | B、3 | C、2 | D、1 |
某程序框图如图所示,则该程序运行后输出的值是( )


| A、0 | B、2013 |
| C、2014 | D、2015 |
函数f(x)=3ax+1-2a在(-1,1)存在一个零点x0,则a的取值范围是( )
A、(-1,
| ||
B、(
| ||
C、(-∞,-1)∪(
| ||
| D、(-∞,-1) |
 如图,矩形ABCD的边长AB=3,BC=2,AE=EF=FB=1,点F处有一弹子球,向BC边撞击,在BC边上随机选择撞击点P,经BC、CD、DA反射后,弹子球落在线段EF上的概率为( )
如图,矩形ABCD的边长AB=3,BC=2,AE=EF=FB=1,点F处有一弹子球,向BC边撞击,在BC边上随机选择撞击点P,经BC、CD、DA反射后,弹子球落在线段EF上的概率为( )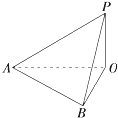 如图,地面上有一旗杆OP,为了测得它的高度,在地面上选一基线AB,测得AB=20m,在A处测得点P的仰角为30°,在B处测得点P的仰角为45°,同时可测得∠AOB=60°,求旗杆的高度(结果保留1位小数).
如图,地面上有一旗杆OP,为了测得它的高度,在地面上选一基线AB,测得AB=20m,在A处测得点P的仰角为30°,在B处测得点P的仰角为45°,同时可测得∠AOB=60°,求旗杆的高度(结果保留1位小数).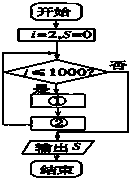 根据条件填空,把求1~1 000内所有偶数的和的程序框图补充完整.①
根据条件填空,把求1~1 000内所有偶数的和的程序框图补充完整.①