题目内容
已知集合A={x|x∈R|(a2-1)x2+(a+1)x+1=0}中有且仅有一个元素,求a的值.
考点:元素与集合关系的判断
专题:计算题,集合
分析:将题目条件转化为方程有且只有一个根,注意讨论方程次数.
解答:
解:∵集合A={x|x∈R|(a2-1)x2+(a+1)x+1=0}中有且仅有一个元素,
∴方程(a2-1)x2+(a+1)x+1=0有且只有一个实数根;
∴①当a2-1=0,a+1≠0时,
a=1;
②当a2-1≠0,
(a+1)2-4×(a2-1)=0
解得,a=-1(舍去)或a=
;
∴a=1或
.
∴方程(a2-1)x2+(a+1)x+1=0有且只有一个实数根;
∴①当a2-1=0,a+1≠0时,
a=1;
②当a2-1≠0,
(a+1)2-4×(a2-1)=0
解得,a=-1(舍去)或a=
| 5 |
| 3 |
∴a=1或
| 5 |
| 3 |
点评:本题考查了集合与元素关系的判断,属于基础题.

练习册系列答案
相关题目
若f(x)=x2+bx+c,且f(1)=0,f(2)=0,则f(-1)=( )
| A、6 | B、-6 | C、5 | D、-5 |
某程序框图如图所示,则该程序运行后输出的值是( )


| A、0 | B、2013 |
| C、2014 | D、2015 |
 如图,矩形ABCD的边长AB=3,BC=2,AE=EF=FB=1,点F处有一弹子球,向BC边撞击,在BC边上随机选择撞击点P,经BC、CD、DA反射后,弹子球落在线段EF上的概率为( )
如图,矩形ABCD的边长AB=3,BC=2,AE=EF=FB=1,点F处有一弹子球,向BC边撞击,在BC边上随机选择撞击点P,经BC、CD、DA反射后,弹子球落在线段EF上的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
执行如图所示的程序框图,输出的S值为( )


| A、8 | B、6 | C、4 | D、2 |
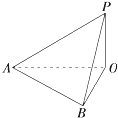 如图,地面上有一旗杆OP,为了测得它的高度,在地面上选一基线AB,测得AB=20m,在A处测得点P的仰角为30°,在B处测得点P的仰角为45°,同时可测得∠AOB=60°,求旗杆的高度(结果保留1位小数).
如图,地面上有一旗杆OP,为了测得它的高度,在地面上选一基线AB,测得AB=20m,在A处测得点P的仰角为30°,在B处测得点P的仰角为45°,同时可测得∠AOB=60°,求旗杆的高度(结果保留1位小数). 如图,AB是半圆O的直径,C是半圆O上异于A,B的点,CD⊥AB,垂足为D.若AD=2,BC=2
如图,AB是半圆O的直径,C是半圆O上异于A,B的点,CD⊥AB,垂足为D.若AD=2,BC=2