题目内容
 的内角
的内角 所对的边分别为
所对的边分别为 ,向量
,向量 与
与 平行.
平行.
(I)求 ;
;
(II)若 求
求 的面积.
的面积.
(I)  ;(II)
;(II)  .
.
(I)因为 ,所以
,所以
由正弦定理,得 ,
,
又 ,从而
,从而 ,
,
由于
所以
(II)解法一:由余弦定理,得
 ,而
,而 ,
, ,
,
得 ,即
,即
因为 ,所以
,所以 ,[来源:学|科|网Z|X|X|K]
,[来源:学|科|网Z|X|X|K]
故 面积为
面积为 .
.
解法二:由正弦定理,得
从而
又由 知
知 ,所以
,所以
故
 ,
,
所以 面积为
面积为 .
.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
 ,表示的平面区域为三角形,且其面积等于
,表示的平面区域为三角形,且其面积等于 ,则m的值为
,则m的值为 的展开式中,
的展开式中, 的系数为
的系数为  B.
B. C.
C. D.
D.


 ,若
,若 ,则
,则 的概率( )
的概率( ) B.
B.  C.
C. D.
D. 
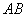 切
切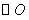 于点
于点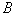 ,直线
,直线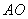 交
交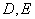 两点,
两点,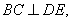 垂足为
垂足为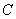 .
.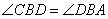
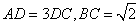 ,求
,求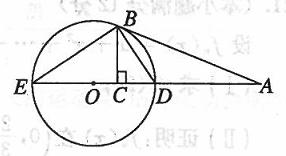
 C. 2 D.
C. 2 D. 

 ;
; (2)
(2) .
. .以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M.
.以AB为直径的圆O交AC于点E,点D是BC边的中点,连接OD交圆O于点M.
