题目内容
10.设向量$\overrightarrow a,\overrightarrow b$满足$|{\overrightarrow a}|=|{\overrightarrow b}$|=1,$\overrightarrow a•\overrightarrow b=m$,则$|{\overrightarrow a+t\overrightarrow b}|({t∈R})$的最小值为( )| A. | 2 | B. | $\sqrt{1+{m^2}}$ | C. | 1 | D. | $\sqrt{1-{m^2}}$ |
分析 根据向量的数量积公式和向向量的模的以及二次函数的性质即可求出.
解答 解:∵$|{\overrightarrow a}|=|{\overrightarrow b}$|=1,$\overrightarrow a•\overrightarrow b=m$,
∴|$\overrightarrow{a}$+t$\overrightarrow{b}$|2=|$\overrightarrow{a}$|2+2t$\overrightarrow{a}$•$\overrightarrow{b}$+t2|$\overrightarrow{b}$|2=1+2tm+t2=(t+m)2-m2+1,
∴|$\overrightarrow{a}$+t$\overrightarrow{b}$|≥$\sqrt{1-{m}^{2}}$
故选:D.
点评 本题主要考查平面向量的模长公式,两个向量的数量积的定义,二次函数的性质,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.已知椭圆C1,抛物线C2的焦点均在x轴上,从两条曲线上各取两个点,将其坐标混合记录于如表中:
(1)求椭圆C1和抛物线C2的标准方程.
(2)过椭圆C1右焦点F的直线l与此椭圆相交于A,B两点,若点P为直线x=4上任意一点,
①试证:直线PA,PF,PB的斜率成等差数列.
②若点P在X轴上,设$\overrightarrow{FA}$=λ$\overrightarrow{FB}$,λ∈[-2,-1],求|$\overrightarrow{PA}$+$\overrightarrow{PB}$|取最大值时的直线l的方程.
| x | -2 | 2 | $\sqrt{6}$ | 9 |
| y | $\sqrt{2}$ | -$\sqrt{2}$ | -1 | 3 |
(2)过椭圆C1右焦点F的直线l与此椭圆相交于A,B两点,若点P为直线x=4上任意一点,
①试证:直线PA,PF,PB的斜率成等差数列.
②若点P在X轴上,设$\overrightarrow{FA}$=λ$\overrightarrow{FB}$,λ∈[-2,-1],求|$\overrightarrow{PA}$+$\overrightarrow{PB}$|取最大值时的直线l的方程.
18.定积分${∫}_{0}^{π}$|sinx-cosx|dx的值是( )
| A. | 2+$\sqrt{2}$ | B. | 2-$\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
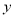 关于月份
关于月份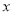 的线性回归方程;
的线性回归方程;
 ,
,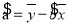 .
. 
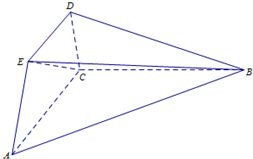 如图,已知平面ABC⊥平面ACDE,且△ABC为等腰直角三角形,AC=BC=4,等腰梯形ACDE中,AC∥DE且AE=DE=2.
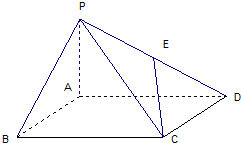
如图,已知平面ABC⊥平面ACDE,且△ABC为等腰直角三角形,AC=BC=4,等腰梯形ACDE中,AC∥DE且AE=DE=2. 如图,在四棱锥P-ABCD中,E为AD上一点,面PAD⊥面ABCD,四边形
如图,在四棱锥P-ABCD中,E为AD上一点,面PAD⊥面ABCD,四边形