题目内容
8.已知向量$\overrightarrow a$=(1,2),$\overrightarrow b$=(x,1).(1)若$\overrightarrow a∥\overrightarrow b$,求x的值;
(2)若<$\overrightarrow{a}$,$\overrightarrow{b}$>为锐角,求x的范围;
(3)当($\overrightarrow a+2\overrightarrow b$)⊥(2$\overrightarrow a-\overrightarrow b$)时,求x的值.
分析 (1)根据平面向量的共线定理,列出方程求得x的值;
(2)当<$\overrightarrow{a}$,$\overrightarrow{b}$>为锐角时,$\overrightarrow a•\overrightarrow b>0$,且$\overrightarrow a,\overrightarrow b$不同向,由此求出x的取值范围;
(3)利用($\overrightarrow a+2\overrightarrow b$)⊥(2$\overrightarrow a-\overrightarrow b$)时数量积为0,列出方程求出x的值.
解答 解:(1)∵向量$\overrightarrow a$=(1,2),$\overrightarrow b$=(x,1),且$\overrightarrow a∥\overrightarrow b$,
∴1×1-2x=0,解得x=$\frac{1}{2}$;
(2)当<$\overrightarrow{a}$,$\overrightarrow{b}$>为锐角时,$\overrightarrow a•\overrightarrow b>0$,且$\overrightarrow a,\overrightarrow b$不同向,
即$\overrightarrow{a}$•$\overrightarrow{b}$=x+2>0,解得x>-2;
又当$x=\frac{1}{2}$时,$\overrightarrow a,\overrightarrow b$同向,
∴x的取值范围是x>-2且$x≠\frac{1}{2}$;
(3)$\overrightarrow a+2\overrightarrow b=(1+2x,4)$,
$(2\overrightarrow a-\overrightarrow b)=(2-x,3)$;
当($\overrightarrow a+2\overrightarrow b$)⊥(2$\overrightarrow a-\overrightarrow b$)时,
(2x+1)(2-x)+3×4=0,
即-2×2+3x+14=0,
解得:$x=\frac{7}{2}$或x=-2.
点评 本题考查了平面向量的坐标运算与数量积运算的应用问题,是基础题目.

 名校课堂系列答案
名校课堂系列答案| A. | 6 | B. | 12 | C. | 18 | D. | 24 |
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{{3\sqrt{3}}}{4}$ | D. | $2\sqrt{3}$ |
| A. | {x|x<1} | B. | {x|x>1} | C. | {x|0<x<1} | D. | ∅ |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
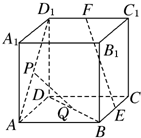 如图,在棱长为a的正方体ABCD-A1B1C1D1中,E,F,P,Q分别是BC,C1D1,AD1,BD的中点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,E,F,P,Q分别是BC,C1D1,AD1,BD的中点.