题目内容
16.已知数列{an}的首项为2,数列{bn}为等比数列且bn=$\frac{{{a_{n+1}}}}{a_n}$,若b11•b12=2,则a23=4096.分析 由于数列{bn}为等比数列且bn=$\frac{{{a_{n+1}}}}{a_n}$,可得b1b2…•b22=$\frac{{a}_{2}}{{a}_{1}}•\frac{{a}_{3}}{{a}_{2}}$•…•$\frac{{a}_{23}}{{a}_{22}}$=$({b}_{11}•{b}_{12})^{11}$,化简代入即可得出.
解答 解:∵数列{bn}为等比数列且bn=$\frac{{{a_{n+1}}}}{a_n}$,
∴b1b2…b22=$\frac{{a}_{2}}{{a}_{1}}•\frac{{a}_{3}}{{a}_{2}}$•…•$\frac{{a}_{23}}{{a}_{22}}$=$\frac{{a}_{23}}{2}$=$({b}_{11}•{b}_{12})^{11}$=211,
∴a23=212=4096.
故答案为:4096.
点评 本题考查了等比数列的通项公式及其性质、递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
7.某人忘记了密码的最后两个数字,只记得这两个数字是不超过5的奇数,则输入一次就正确的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{12}$ |
11.已知等比数列{an}的公比为2,前n项和为Sn,且S1,S2,S3-2成等差数列,则a4=( )
| A. | 8 | B. | $\frac{1}{8}$ | C. | 16 | D. | $\frac{1}{16}$ |
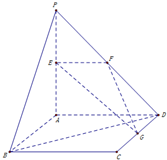 如图,平面PAD⊥平面ABCD,ABCD是正方形,∠PAD=90°,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.
如图,平面PAD⊥平面ABCD,ABCD是正方形,∠PAD=90°,且PA=AD=2,E、F、G分别是线段PA、PD、CD的中点.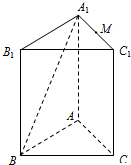 如图,在三棱柱ABC-A1B1C1中,侧棱AA1与底面ABC成角为θ,AB⊥AC.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1与底面ABC成角为θ,AB⊥AC.