题目内容
46.某校高一某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,(阴影部分为破坏部分)其可见部分如下,据此解答如下问题:
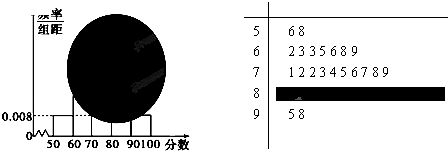
(Ⅰ)计算频率分布直方图中[80,90)间的矩形的高;
(Ⅱ)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份的分数在[90,100]之间的概率;
(Ⅲ)根据频率分布直方图估计这次测试的平均分.

(Ⅰ)计算频率分布直方图中[80,90)间的矩形的高;
(Ⅱ)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份的分数在[90,100]之间的概率;
(Ⅲ)根据频率分布直方图估计这次测试的平均分.
考点:频率分布直方图,古典概型及其概率计算公式
专题:概率与统计
分析:(Ⅰ)先求出样本容量,再求[80,90)间的频数与频率,计算对应矩形的高;
(Ⅱ)求出分数在[80,100]之间的试卷数,用列举法求出基本事件数,计算概率即可;
(Ⅲ)根据频率分布直方图计算这次测试的平均分即可.
(Ⅱ)求出分数在[80,100]之间的试卷数,用列举法求出基本事件数,计算概率即可;
(Ⅲ)根据频率分布直方图计算这次测试的平均分即可.
解答:
解:(Ⅰ)根据题意,频率分布直方图中[50,60)间的频率是0.008×10=0.08,
频数是2,
样本容量是
=25;
∵[80,90)间的频数是25-2-7-10-2=4,
∴频率是
=0.16,
∴矩形的高
=0.016;
(Ⅱ)分数在[80,100]之间的试卷数是4+2=6,分别记为a、b、c、d、A、B;
从这6份中任取2份,ab、ac、ad、aA、aB、bc、bd、bA、bB、cd、cA、cB、dA、dB、AB共15种,
其中至少有一份的分数在[90,100]之间的基本事件数是aA、aB、bA、bB、cA、cB、dA、dB、AB共9种
∴它的概率为P=
=
;
(Ⅲ)根据频率分布直方图计算这次测试的平均分是
=55×0.008×10+65×
+75×
+85×
+95×
=73.8,
由此估计平均分是73.8.
频数是2,
样本容量是
| 2 |
| 0.08 |
∵[80,90)间的频数是25-2-7-10-2=4,
∴频率是
| 4 |
| 25 |
∴矩形的高
| 0.16 |
| 10 |
(Ⅱ)分数在[80,100]之间的试卷数是4+2=6,分别记为a、b、c、d、A、B;
从这6份中任取2份,ab、ac、ad、aA、aB、bc、bd、bA、bB、cd、cA、cB、dA、dB、AB共15种,
其中至少有一份的分数在[90,100]之间的基本事件数是aA、aB、bA、bB、cA、cB、dA、dB、AB共9种
∴它的概率为P=
| 9 |
| 15 |
| 3 |
| 5 |
(Ⅲ)根据频率分布直方图计算这次测试的平均分是
. |
| x |
| 7 |
| 25 |
| 10 |
| 25 |
| 4 |
| 25 |
| 2 |
| 25 |
由此估计平均分是73.8.
点评:本题考查了样本容量与频数、频率的计算问题,也考查了古典概型的概率计算问题,利用频率分布直方图求平均数的问题,是综合题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
已知双曲线x2-y2=a2及其上一点P,求证:
(1)离心率e=
,渐近线方程为y=±x;
(2)P到它的两个焦点的距离的积等于P到双曲线中心距离的平方;
(3)过P作两渐近线的垂线,构成的矩形面积为定值.
(1)离心率e=
| 2 |
(2)P到它的两个焦点的距离的积等于P到双曲线中心距离的平方;
(3)过P作两渐近线的垂线,构成的矩形面积为定值.
已知sinα cosα=
,则sinα+cosα=( )
| 1 |
| 2 |
| A、2 | ||
| B、0 | ||
C、
| ||
D、±
|
已知函数f(x)=
,若|f(x)|≥2m,则m的取值范围是( )
|
| A、[-2,0] |
| B、(-∞,0] |
| C、[-2,1] |
| D、[-1,0] |