题目内容
9.已知定圆M:(x+$\sqrt{3}$)2+y2=16,动圆N过点F($\sqrt{3}$,0)且与圆M相切,记圆心N的轨迹为C直线l过点E(-1,0)且与C于A,B(Ⅰ)求轨迹C方程;
(Ⅱ)△AOB是否存在最大值,若存在,求出△AOB的最大值;若不存在,说明理由.
分析 (Ⅰ)由椭圆定义可知,点P的轨迹C是以N,F为焦点,长半轴长为2的椭圆,由此能求出曲线C的方程.
(Ⅱ)存在△AOB面积的最大值.由直线l过点E(-1,0),设直线l的方程为 x=my-1,联立椭圆方程,整理得(m2+4)y2-2my-3=0.由△=(2m)2+12(m2+4)>0.设A(x1,y1),B(x2,y2).解得y1=$\frac{m+2\sqrt{{m}^{2}+3}}{{m}^{2}+4}$,y2=$\frac{m-2\sqrt{{m}^{2}+3}}{{m}^{2}+4}$.再换元,结合函数的单调性,由此能求出S△AOB的最大值.
解答 解:( I)易知点F($\sqrt{3}$,0)在圆M:(x+$\sqrt{3}$)2+y2=16内,所以圆N内切于圆M,又圆M的半径为4,所以|NM|+|NF|=4>2$\sqrt{3}$=|FM|,所以点N的轨迹C为椭圆,且2a=4,c=$\sqrt{3}$,所以b=1,
所以轨迹C的方程为$\frac{{x}^{2}}{4}+{y}^{2}$=1 (4分)
(Ⅱ)存在△AOB面积的最大值.…(6分)
因为直线l过点E(-1,0),设直线l的方程为 x=my-1或y=0(舍).
联立椭圆方程,整理得 (m2+4)y2-2my-3=0.…(7分)
由△=(2m)2+12(m2+4)>0.
设A(x1,y1),B(x2,y2).
解得y1=$\frac{m+2\sqrt{{m}^{2}+3}}{{m}^{2}+4}$,y2=$\frac{m-2\sqrt{{m}^{2}+3}}{{m}^{2}+4}$.
则|y2-y1|=$\frac{4\sqrt{{m}^{2}+3}}{{m}^{2}+4}$.
∴S△AOB=$\frac{1}{2}$|OE||y2-y1|=$\frac{2}{\sqrt{{m}^{2}+3}+\frac{1}{\sqrt{{m}^{2}+3}}}$ …(10分)
设g(t)=t+$\frac{1}{t}$,t=$\sqrt{{m}^{2}+3}$,t≥$\sqrt{3}$.
则g(t)在区间[$\sqrt{3}$,+∞)上为增函数.
所以g(t)≥$\frac{4\sqrt{3}}{3}$.
所以S△AOB≤$\frac{\sqrt{3}}{2}$,
当且仅当m=0时取等号,所以S△AOB的最大值为$\frac{\sqrt{3}}{2}$.…(13分)
点评 本题考查曲线的轨迹方程的求法,考查三角形的面积的最大值的求法,解题时要认真审题,注意等价转化思想的合理运用.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案| A. | 42 | B. | 44 | C. | 46 | D. | 48 |
| A. | n=45,p=$\frac{2}{3}$ | B. | n=45,p=$\frac{1}{3}$ | C. | n=90,p=$\frac{1}{3}$ | D. | n=90,p=$\frac{2}{3}$ |
| A. | 命题“若x=1,则x2+x-2=0”的否命题是假命题 | |
| B. | 命题“存在一个实数x,使不等式x2-3x+4<0成立”为真命题 | |
| C. | 命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” | |
| D. | 过点(0,2)与抛物线y2=8x只有一个公共点的直线有3条 |
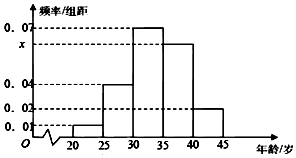 为增强市民的节能环保意识,郑州市面向全市征召义务宣传志愿者,从符合条件的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示,其中年龄分组区是:[20,25],[25,30],[30,35],[35,40],[40,45].
为增强市民的节能环保意识,郑州市面向全市征召义务宣传志愿者,从符合条件的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示,其中年龄分组区是:[20,25],[25,30],[30,35],[35,40],[40,45].