题目内容
设关于x的函数f(x)=x2+ax-b,从集合A={x|0≤x≤3}中任取一个元素为a,从集合B={x|0≤x≤2}中任取一个元素为b,则使f(1)≥1的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:计算题,作图题,概率与统计
分析:由题意,f(1)≥1可化为a-b≥0;可知符合几何概型,作图求面积比即可.
解答:
解:由题意,f(1)≥1可化为1+a-b≥1;
故a-b≥0;
由题意可知符合几何概型,
作出其平面区域如下,

S阴=2×3-
×2×2=4;
故使f(1)≥1的概率为
=
;
故选A.
故a-b≥0;
由题意可知符合几何概型,
作出其平面区域如下,

S阴=2×3-
| 1 |
| 2 |
故使f(1)≥1的概率为
| 4 |
| 2×3 |
| 2 |
| 3 |
故选A.
点评:本题考查了几何概型的应用及作图能力,属于基础题.

练习册系列答案
相关题目
方程(x-y)2+(xy-1)2=0的曲线是( )
| A、一条直线和一条双曲线 |
| B、两条双曲线 |
| C、两个点 |
| D、以上答案都不对 |
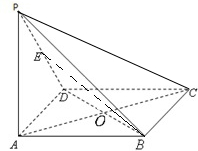 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB= 如图,PA⊥平面AC,四边形ABCD是矩形,E,F分别是AB,PD的中点.
如图,PA⊥平面AC,四边形ABCD是矩形,E,F分别是AB,PD的中点.