题目内容
已知函数f(x)=2alnx-x+
,a≠0,g(x)=-x2-x+2
b.
(1)若函数f(x)在定义域上有极值,求实数a的取值范围?
(2)当a=
时,对?x0∈[1,e],总存在t∈[1,e]使f(x0)<g(t)成立,求实数b的范围.
| 1 |
| x |
| 2 |
(1)若函数f(x)在定义域上有极值,求实数a的取值范围?
(2)当a=
| 2 |
考点:利用导数研究函数的极值,利用导数求闭区间上函数的最值
专题:计算题,导数的综合应用
分析:(1)由题意,f(x)=2alnx-x+
的定义域为(0,+∞);f′(x)=
-1-
=
;函数f(x)在定义域上有极值化为导数有正有负,故讨论a即可,从而求a;
(2)当a=
时,f′(x)=
;从而求出fmax(x)=f(
+1)=2
ln(
+1)-2;从而可得总存在t∈[1,e]使2
ln(
+1)-2<g(t)成立;再求gmax(t)=g(1)=-2+2
b;从而可得2
ln(
+1)-2<-2+2
b;从而解得.
| 1 |
| x |
| 2a |
| x |
| 1 |
| x2 |
| -x2+2ax-1 |
| x2 |
(2)当a=
| 2 |
-(x-
| ||
| x2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
解答:
解:(1)f(x)=2alnx-x+
的定义域为(0,+∞);
f′(x)=
-1-
=
;
①当a<0时,f′(x)<0;
故f(x)在定义域上为减函数,故无极值;
当a>0时,
若函数f(x)在定义域上有极值,
则
解得a>1;
故实数a的取值范围为(1,+∞);
(2)当a=
时,f′(x)=
;
故f(x)在[1,
+1]上是增函数,在[
+1,e]上是减函数;
故fmax(x)=f(
+1)=2
ln(
+1)-2;
则对?x0∈[1,e],总存在t∈[1,e]使f(x0)<g(t)成立可化为
总存在t∈[1,e]使2
ln(
+1)-2<g(t)成立;
又∵g(x)=-x2-x+2
b在[1,e]上是减函数,
故gmax(t)=g(1)=-2+2
b;
故2
ln(
+1)-2<-2+2
b;
故b>ln(
+1).
| 1 |
| x |
f′(x)=
| 2a |
| x |
| 1 |
| x2 |
| -x2+2ax-1 |
| x2 |
①当a<0时,f′(x)<0;
故f(x)在定义域上为减函数,故无极值;
当a>0时,
若函数f(x)在定义域上有极值,
则
|
解得a>1;
故实数a的取值范围为(1,+∞);
(2)当a=
| 2 |
-(x-
| ||
| x2 |
故f(x)在[1,
| 2 |
| 2 |
故fmax(x)=f(
| 2 |
| 2 |
| 2 |
则对?x0∈[1,e],总存在t∈[1,e]使f(x0)<g(t)成立可化为
总存在t∈[1,e]使2
| 2 |
| 2 |
又∵g(x)=-x2-x+2
| 2 |
故gmax(t)=g(1)=-2+2
| 2 |
故2
| 2 |
| 2 |
| 2 |
故b>ln(
| 2 |
点评:本题考查了导数的综合应用及恒成立问题及存在性问题的处理方法,属于中档题.

练习册系列答案
相关题目
等比数列{an}中,a6=2,a5=5,则数列{lgan}的前10项和等于( )
| A、6 | B、5 | C、4 | D、3 |
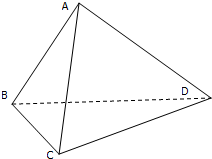 如图所示,空间四边形ABCD中,平面ABD⊥平面BCD,∠BAD=90°,∠BCD=90°,且AB=AD,则AC与平面BCD所成的角为
如图所示,空间四边形ABCD中,平面ABD⊥平面BCD,∠BAD=90°,∠BCD=90°,且AB=AD,则AC与平面BCD所成的角为