题目内容
9．已知tanθ=3，则cos（$\frac{3π}{2}$+2θ）=（ ）| A． | -$\frac{4}{5}$ | B． | -$\frac{3}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
分析 利用诱导公式、同角三角函数的基本关系，求得式子cos（$\frac{3π}{2}$+2θ）的值．
解答 解：∵tanθ=3，则cos（$\frac{3π}{2}$+2θ）=sin2θ=$\frac{2sinθcosθ}{{sin}^{2}θ{+cos}^{2}θ}$=$\frac{2tanθ}{{tan}^{2}θ+1}$=$\frac{6}{9+1}$=$\frac{3}{5}$，
故选：C．
点评 本题主要考查同角三角函数的基本关系、诱导公式的应用，属于基础题．
练习册系列答案
相关题目
19．设直线m，n是两条不同的直线，α，β是两个不同的平面，下列事件中是必然事件的是（ ）
| A． | 若m∥α，n∥β，m⊥n，则α⊥β | B． | 若m∥α，n⊥β，m∥n，则α∥β | ||
| C． | 若m⊥α，n∥β，m⊥n，则α∥β | D． | 若m⊥α，n⊥β，m∥n，则α∥β |
20．
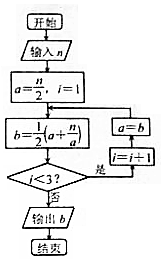一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图，若输入的n=12，则输出的结果b=（ ）
一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图，若输入的n=12，则输出的结果b=（ ）| A． | 4 | B． | $\frac{7}{2}$ | C． | $\frac{97}{28}$ | D． | $\frac{64}{14}$ |
17．已知函数f（x）=$\frac{1+lnx}{x}$，若关于x的不等式f2（x）+af（x）＞0恰有两个整数解，则实数a的取值范围是（ ）
| A． | （-$\frac{1+ln2}{2}$，-$\frac{1+ln3}{3}$） | B． | [$\frac{1+ln3}{3}$，$\frac{1+ln2}{2}$） | C． | （-$\frac{1+ln2}{2}$，-$\frac{1+ln3}{3}$] | D． | （-1，-$\frac{1+ln3}{3}$] |
14．已知函数f（x）=$\left\{\begin{array}{l}{lnx，x＞1}\\{1-{x}^{3}，x≤1}\end{array}\right.$，若函数y=f（x）-a（x-1）恰有三个零点，则实数a的取值范围是（ ）
| A． | （-$\frac{3}{4}$，0） | B． | （-∞，-$\frac{3}{4}$） | C． | （-3，-$\frac{3}{4}$） | D． | （0，1） |
1．双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的左、右焦点分别为F1，F2，过F1作x轴的垂线交双曲线于A，B两点，若$∠A{F_2}B＜\frac{π}{3}$，则双曲线离心率的取值范围是（ ）
| A． | $（{1，\sqrt{3}}）$ | B． | $（{1，\sqrt{6}}）$ | C． | $（{1，2\sqrt{3}}）$ | D． | $（{\sqrt{3}，3\sqrt{3}}）$ |
18．在等差数列{an}中，Sn为其前n项和，若a3+a4+a8=25，则S9=（ ）
| A． | 60 | B． | 75 | C． | 90 | D． | 105 |