题目内容
20．
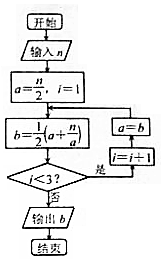一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图，若输入的n=12，则输出的结果b=（ ）| A． | 4 | B． | $\frac{7}{2}$ | C． | $\frac{97}{28}$ | D． | $\frac{64}{14}$ |
分析 根据已知中的流程图，我们模拟程序的运行结果，看变量i的值是否满足判断框的条件，当判断框的条件不满足时执行循环，满足时退出循环，即可得到输出结果．
解答 解：模拟程序的运行，可得
n=12，a=6，i=1
b=4
满足条件i＜3，执行循环体，i=2，a=4，b=$\frac{7}{2}$，
满足条件i＜3，执行循环体，i=3，a=$\frac{7}{2}$，b=$\frac{97}{28}$，
不满足条件i＜3，退出循环，输出b的值为$\frac{97}{28}$．
故选：C．
点评 本题主要考查的知识点是程序框图，模拟循环的执行过程是解答此类问题常用的办法，属于基础题．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
12．掷一枚均匀的硬币4次，出现正面向上的次数不少于反面向上的次数的概率为（ ）
| A． | $\frac{5}{16}$ | B． | $\frac{1}{2}$ | C． | $\frac{5}{8}$ | D． | $\frac{11}{16}$ |
9．已知tanθ=3，则cos（$\frac{3π}{2}$+2θ）=（ ）
| A． | -$\frac{4}{5}$ | B． | -$\frac{3}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
10．
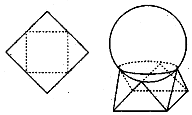如图所示，用一边长为$\sqrt{2}$的正方形硬纸，按各边中点垂直折起四个小三角形，做成一个蛋巢，将体积为$\frac{4π}{3}$的鸡蛋（视为球体）放入其中，蛋巢形状保持不变，则鸡蛋（球体）离蛋巢底面的最短距离为（ ）
如图所示，用一边长为$\sqrt{2}$的正方形硬纸，按各边中点垂直折起四个小三角形，做成一个蛋巢，将体积为$\frac{4π}{3}$的鸡蛋（视为球体）放入其中，蛋巢形状保持不变，则鸡蛋（球体）离蛋巢底面的最短距离为（ ）| A． | $\frac{\sqrt{2}-1}{2}$ | B． | $\frac{\sqrt{2}+1}{2}$ | C． | $\frac{\sqrt{6}-1}{2}$ | D． | $\frac{\sqrt{3}-1}{2}$ |