题目内容
1.双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点分别为F1,F2,过F1作x轴的垂线交双曲线于A,B两点,若$∠A{F_2}B<\frac{π}{3}$,则双曲线离心率的取值范围是( )| A. | $({1,\sqrt{3}})$ | B. | $({1,\sqrt{6}})$ | C. | $({1,2\sqrt{3}})$ | D. | $({\sqrt{3},3\sqrt{3}})$ |
分析 直接利用双曲线的通径与$∠A{F_2}B<\frac{π}{3}$,得到a,b,c的关系,运用离心率公式,求出双曲线的离心率的范围.
解答 解:由题意可知,双曲线的通径为:$\frac{2{b}^{2}}{a}$,
因为过焦点F1且垂直于x轴的弦为AB,若$∠A{F_2}B<\frac{π}{3}$,
所以$\frac{\frac{{b}^{2}}{a}}{2c}$=tan∠AF2B<$\frac{\sqrt{3}}{3}$,e=$\frac{c}{a}$>1,
所以$\frac{{c}^{2}-{a}^{2}}{2ac}<\frac{\sqrt{3}}{3}$,$\frac{1}{2}e-\frac{1}{2e}<\frac{\sqrt{3}}{3}$,由解得e∈(1,$\sqrt{3}$).
故选:A.
点评 本题考查双曲线的基本性质,双曲线的离心率的求法,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.掷一枚均匀的硬币4次,出现正面向上的次数不少于反面向上的次数的概率为( )
| A. | $\frac{5}{16}$ | B. | $\frac{1}{2}$ | C. | $\frac{5}{8}$ | D. | $\frac{11}{16}$ |
9.已知tanθ=3,则cos($\frac{3π}{2}$+2θ)=( )
| A. | -$\frac{4}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
10.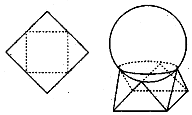 如图所示,用一边长为$\sqrt{2}$的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为$\frac{4π}{3}$的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋(球体)离蛋巢底面的最短距离为( )
如图所示,用一边长为$\sqrt{2}$的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为$\frac{4π}{3}$的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋(球体)离蛋巢底面的最短距离为( )
 如图所示,用一边长为$\sqrt{2}$的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为$\frac{4π}{3}$的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋(球体)离蛋巢底面的最短距离为( )
如图所示,用一边长为$\sqrt{2}$的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为$\frac{4π}{3}$的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋(球体)离蛋巢底面的最短距离为( )| A. | $\frac{\sqrt{2}-1}{2}$ | B. | $\frac{\sqrt{2}+1}{2}$ | C. | $\frac{\sqrt{6}-1}{2}$ | D. | $\frac{\sqrt{3}-1}{2}$ |
 如图所示,在正方体ABCD-A1B1C1D1中,AB=4,M,N分别为棱A1D1,A1B1的中点,过点B的平面α∥平面AMN,则平面α截该正方体所得截面的面积为18.
如图所示,在正方体ABCD-A1B1C1D1中,AB=4,M,N分别为棱A1D1,A1B1的中点,过点B的平面α∥平面AMN,则平面α截该正方体所得截面的面积为18.