题目内容
12.{an}为正项数列,a1=2,an+1=an+2$\sqrt{{a}_{n}}$+1,求an的通项公式.分析 根据数列递推式,变形可得数列{$\sqrt{{a}_{n}}$}是以$\sqrt{2}$为首项,以1为公差的等差数列,由此可得结论.
解答 解::an+1=an+2$\sqrt{{a}_{n}}$+1,
∴an+1=($\sqrt{{a}_{n}}$+1)2,
∵{an}为正项数列,
∴$\sqrt{{a}_{n+1}}$=$\sqrt{{a}_{n}}$+1,
∴$\sqrt{{a}_{n+1}}$-$\sqrt{{a}_{n}}$=1,
∵a1=2,
∴$\sqrt{{a}_{1}}$=$\sqrt{2}$,
∴{$\sqrt{{a}_{n}}$}是以$\sqrt{2}$为首项,以1为公差的等差数列,
∴$\sqrt{{a}_{n}}$=$\sqrt{2}$+(n-1),
∴an=(n-1)2+2+2$\sqrt{2}$(n-1).
点评 本题考查数列递推式,考查等差数列的判定,考查学生的计算能力,属于中档题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
3.已知tanαcosα>0且cotαsinα<0,则α是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20.f(x)=xcosx-5sinx+2,若f(2)=7,则f(-2)的值为( )
| A. | -7 | B. | 9 | C. | -5 | D. | -3 |
7.函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则f(-$\frac{π}{2}$)=( )
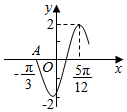
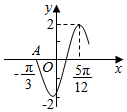
| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | 1 | D. | -1 |
4.设向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足$\overrightarrow{a}$$+\overrightarrow{b}$$+\overrightarrow{c}$=$\overrightarrow{0}$,且|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2,|$\overrightarrow{c}$|=4,则$\overrightarrow{a}$$•\overrightarrow{b}$=( )
| A. | 4 | B. | 2$\sqrt{2}$ | C. | 2 | D. | $\sqrt{2}$ |
2.函数f(x)=sin2x+2$\sqrt{3}$cos2x-$\sqrt{3}$,g(x)=mcos(2x-$\frac{π}{6}$)-2m+3(m>0),若对任意x1∈[0,$\frac{π}{4}$],存在x2∈[0,$\frac{π}{4}$],使得g(x1)=f(x2)成立,则实数m的取值范围是( )
| A. | (1,$\frac{4}{3}$) | B. | ($\frac{2}{3}$,1] | C. | [$\frac{2}{3}$,1] | D. | [1,$\frac{4}{3}$] |
 如图,已知在△ABC中,AC的中点为E,AB的中点为F,延长BE至P,使BE=EP,延长CF至Q,使CF=FQ.试用向量方法证明P,A,Q三点共线.
如图,已知在△ABC中,AC的中点为E,AB的中点为F,延长BE至P,使BE=EP,延长CF至Q,使CF=FQ.试用向量方法证明P,A,Q三点共线.