题目内容
已知双曲线C:2x2-
y2=1
(1)求与双曲线C共渐近线且过A(2,-3)点的双曲线方程;x2-
=1
(2)求与双曲线C有相同焦点且经过点(2,-
)的椭圆方程.
+
=1.
| 2 |
| 3 |
(1)求与双曲线C共渐近线且过A(2,-3)点的双曲线方程;x2-
| y2 |
| 3 |
(2)求与双曲线C有相同焦点且经过点(2,-
| 3 |
| x2 |
| 8 |
| y2 |
| 6 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)与2x2-
y2=1有相同的渐近线的方程可设为2x2-
y2=λ≠0,再把点A的坐标代入即可;
(2)确定双曲线C:2x2-
y2=1的焦点坐标为(±
,0),设椭圆方程为
+
=1(m>0),代入点(2,-
),可得椭圆方程.
| 2 |
| 3 |
| 2 |
| 3 |
(2)确定双曲线C:2x2-
| 2 |
| 3 |
| 2 |
| x2 |
| m |
| y2 |
| m-2 |
| 3 |
解答:
解:(1)与双曲线C共渐近线的方程可设为2x2-
y2=λ≠0,代入A(2,-3),
可得λ=2,
∴所求双曲线方程;x2-
=1.
(2)双曲线C:2x2-
y2=1的焦点坐标为(±
,0),
设椭圆方程为
+
=1(m>0),
代入点(2,-
)得
+
=1,由m>0可得m=8,
∴椭圆方程为
+
=1.
| 2 |
| 3 |
可得λ=2,
∴所求双曲线方程;x2-
| y2 |
| 3 |
(2)双曲线C:2x2-
| 2 |
| 3 |
| 2 |
设椭圆方程为
| x2 |
| m |
| y2 |
| m-2 |
代入点(2,-
| 3 |
| 4 |
| m |
| 3 |
| m-2 |
∴椭圆方程为
| x2 |
| 8 |
| y2 |
| 6 |
点评:本题考查双曲线、椭圆的方程,考查学生的计算能力,正确设方程是关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
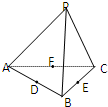 空间四边形PABC的各边及对角线长度都相等,D、E、F分别是AB、BC、CA的中点,下列四个结论中不成立的是( )
空间四边形PABC的各边及对角线长度都相等,D、E、F分别是AB、BC、CA的中点,下列四个结论中不成立的是( )| A、DF∥平面PBC |
| B、AB⊥平面PDC |
| C、平面PEF⊥平面ABC |
| D、平面PAE平面PBC |
 四棱锥P-ABCD中,底面ABCD是边长为8的菱形,∠BAD=
四棱锥P-ABCD中,底面ABCD是边长为8的菱形,∠BAD=