题目内容
18.若a>b>0,c<d<0,则一定有( )| A. | ad>bc | B. | ad<bc | C. | ac>bd | D. | ac<bd |
分析 利用不等式的基本性质即可得出.
解答 解:∵c<d<0,∴-c>-d>0.
又a>b>0,
则一定有-ac>-bd,可得ac<bd.
故选:D.
点评 本题考查了不等式的基本性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
6.在区间[2,10]上任取一个数,这个数在区间[5,7]上的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
8.点P在双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右支上,其左右焦点分别为F1,F2,直线PF1与以坐标原点O为圆心a为半径的圆相切于点A,线段PF1的垂直平分线恰好过点F2,则$\frac{{S}_{△O{F}_{2}A}}{{S}_{△P{F}_{1}{F}_{2}}}$的值为( )
| A. | $\frac{1}{7}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{8}$ |
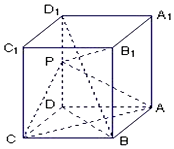 如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P是DD1的中点.
如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P是DD1的中点.