题目内容
如图,在五棱锥P-ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC.∠ABC=45°,AB=2 ,BC=2AE=4,三角形PAB是等腰三角形.
,BC=2AE=4,三角形PAB是等腰三角形.
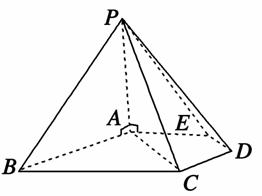
(1)求证:平面PCD⊥平面PAC;
(2)求直线PB与平面PCD所成角的大小;
(3)求四棱锥P-ACDE的体积.
[解析] (1)在△ABC中,因为∠ABC=45°,BC=4,
AB=2 ,
,
所以AC2=AB2+BC2-2AB·BC· cos45°=8,
因此AC=2 ,故BC2=AC2+AB2,
,故BC2=AC2+AB2,
所以∠BAC=90°.
又PA⊥平面ABCDE,AB∥CD,
所以CD⊥PA,CD⊥AC,
又PA,AC平面PAC,且PA∩AC=A,
所以CD⊥平面PAC.
又CD平面PCD,
所以平面PCD⊥平面PAC.
(2)由(1)知AB,AC,AP两两相互垂直,分别以AB、AC、AP为x轴、y轴、z轴建立如图所示的空间直角坐标系,由于△PAB是等腰三角形,所以PA=AB=2 .
.
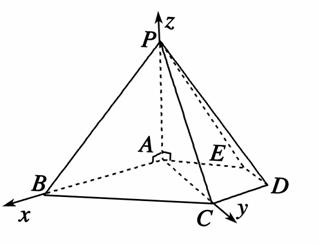
又AC=2 ,
,
因此A(0,0,0),B(2 ,0,0),C(0,2
,0,0),C(0,2 ,0),P(0,0,2
,0),P(0,0,2 ).
).
因为AC∥ED,CD⊥AC,
所以四边形ACDE是直角梯形.
因为AE=2,∠ABC=45°,AE∥BC,
所以∠BAE=135°,因此∠CAE=45°,
故CD=AE·sin45°=2×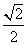 =
= ,
,
所以D(- ,2
,2 ,0).
,0).
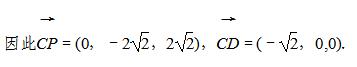
 因此直线PB与平面PCD所成的角为
因此直线PB与平面PCD所成的角为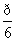 .
.
(3)因为AC∥ED,CD⊥AC,
所以四边形ACDE是直角梯形.
因为AE=2,∠ABC=45°,AE∥BC,
所以∠BAE=135°,因此∠CAE=45°,
故CD=AE·sin45°=2×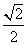 =
= ,
,
ED=AC-AE·cos45°=2 -2×
-2×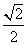 =
= ,
,
所以S四边形ACDE=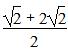 ×
× =3.
=3.
又PA⊥平面ABCDE,
所以VP-ACDE=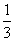 ×3×2
×3×2 =2
=2 .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
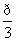 ,则cos<
,则cos<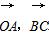 >的值为( )
>的值为( )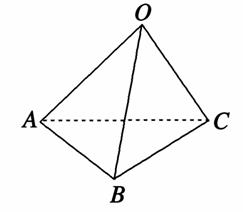
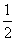
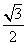 D.
D.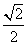
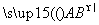 ,
,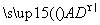 ,
,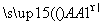 两两的夹角均为60°,且|
两两的夹角均为60°,且|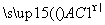 |=( )
|=( )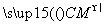 ,
,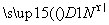 >的值为( )
>的值为( )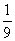 B.
B.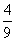
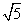
 .
. 上单调递减的是( )
上单调递减的是( ) B.
B. C.
C. D.
D.