题目内容
8.若函数y=x2+2(a-b)x+a2与x轴有两个交点,且b>0,则a与b的关系是( )| A. | a>b | B. | a$<\frac{b}{2}$ | C. | a$>\frac{b}{2}$ | D. | a<b |
分析 转化为方程有两个不同的根,从而可得△=[2(a-b)]2-4a2>0,从而解不等式即可.
解答 解:∵函数y=x2+2(a-b)x+a2与x轴有两个交点,
∴△=[2(a-b)]2-4a2>0,
即(a-b-a)(a-b+a)>0,
即-b(2a-b)>0,
∵b>0,
∴2a-b<0,
∴a<$\frac{b}{2}$,
故选:B.
点评 本题考查了二次函数的性质的应用及二次方程的根的个数的判断,同时考查了转化思想的应用.

练习册系列答案
相关题目
18.若A∈a,B∈a,C是AB上任意一点,则下列结论错误的是( )
| A. | AC?a | B. | BC?a | C. | C?a | D. | C∈a |
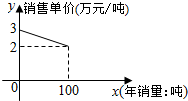 某种产品的成本f1(x)(万元)与年产量x(吨)之间的函数关系是f1(x)=$\frac{1}{100}$x2,该产品的销售单价f2(x)可以表示为关于年销量的一次函数,其部分图象如图所示,且生产的产品都能在当年销售完.
某种产品的成本f1(x)(万元)与年产量x(吨)之间的函数关系是f1(x)=$\frac{1}{100}$x2,该产品的销售单价f2(x)可以表示为关于年销量的一次函数,其部分图象如图所示,且生产的产品都能在当年销售完.